2022-2023学年湖南省长沙市长沙县八年级（下）期末数学试卷

一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．式子

  x

  -

  2

  在实数范围内有意义，则x的取值范围是（　　）

  A．x≥0

  B．x≥-2

  C．x≤2

  D．x≥2
  组卷：382引用：9难度：0.8

  解析

• 2．化简

  （

  -

  2

  ）

  2

  的结果正确的是（　　）

  A．-2

  B．2

  C．±2

  D．4
  组卷：304引用：28难度：0.9

  解析

• 3．如图，数轴上点A表示的实数是（　　）
  

  A． 3

  B． 5

  C．2.5

  D． 6
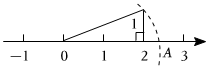  组卷：223引用：4难度：0.9

  解析

• 4．若三条线段a、b、c满足a²+b²-c²=0，这三条线段组成的三角形是（　　）

  A．锐角三角形

  B．直角三角形

  C．钝角三角形

  D．无法判断
  组卷：137引用：1难度：0.9

  解析

• 5．在△ABC中，D，E分别是边AB，AC的中点，若BC=5，则DE的长是（　　）

  A．15

  B．10

  C．5

  D．2.5
  组卷：52引用：1难度：0.9

  解析

• 6．若关于x的一元二次方程x²+2x-k=0有两个不相等的实数根，则k的取值范围是（　　）

  A．k＜-1

  B．k＞-1

  C．k＜1

  D．k＞1
  组卷：1102引用：15难度：0.8

  解析

• 7．在圆锥体积公式

  V

  =

  1

  3

  π

  r

  2

  h

  中（其中，r表示圆锥底面半径，h表示圆锥的高），常量与变量分别是（　　）

  A．常量是 1 3 ， π ，变量是V，h

  B．常量是 1 3 ， π ，变量是h,r

  C．常量是 1 3 ， π ，变量是V，h,r

  D．常量是 1 3 ，变量是V，h,π，r
  组卷：1844引用：12难度：0.7

  解析

• 8．若一次函数y=（m-3）x-3的图象经过第二、三、四象限，则常数m的取值范围是（　　）

  A．m＜3

  B．m＜0

  C．m＞3

  D．m＞-3
  组卷：465引用：5难度：0.5

  解析

三、解答题：本大题共9小题，共72分，解答应写出必要的文字说明、证明过程或演算步骤．

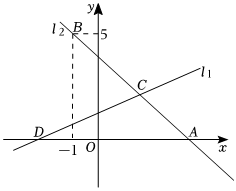• 24．如图，直线l₁：y=kx+1与x轴交于点D，直线l₂：y=-x+b与x轴交于点A，且经过定点B（-1，5），直线l₁与l₂交于点C（2，m）．
  （1）填空：k=

  ；b=

  ；m=

  ；
  （2）在x轴上是否存在一点E，使△BCE的周长最短？若存在，请求出点E的坐标；若不存在，请说明理由：
  （3）若动点P在射线DC上从点D开始以每秒1个单位的速度运动，连接AP，设点P的运动时间为t秒．是否存在t的值，使△ACP和△ADP的面积比为1：2？若存在，直接写出t的值；若不存在，请说明理由．
  组卷：366引用：1难度：0.2

  解析

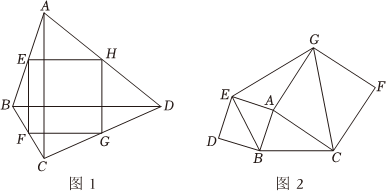• 25．定义：对于一个凸四边形，我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”，如果原四边形的中点四边形是个正方形，我们把这个原四边形叫做“中正四边形”．
  （1）概念理解：下列四边形中一定是“中正四边形”的是

  ；
  A．平行四边形B．矩形C．菱形D．正方形
  （2）性质探究：如图1，四边形ABCD是“中正四边形”，观察图形，直接写出关于四边形ABCD对角线的两条结论；
  （3）问题解决：如图2，△ABC为锐角三角形，以△ABC的两边AB，AC为边长，分别向外侧作正方形ABDE和正方形ACFG，连接BE，EG，GC．求证：四边形BCGE是“中正四边形”．
  组卷：178引用：4难度：0.3

  解析