2022-2023学年广东省东莞市嘉荣外国语学校八年级（下）期中数学试卷

一、选择题（本大题共10小题，共30.0分。）

• 1．式子

  x

  -

  2

  在实数范围内有意义，则x的取值范围是（　　）

  A．x≥0

  B．x≤2

  C．x≥-2

  D．x≥2
  组卷：1103引用：28难度：0.9

  解析

• 2．若

  a

  +

  1

  +

  b

  -

  1

  =

  0

  ，则a¹⁰¹¹+b¹⁰¹¹的值等于（　　）

  A．2

  B．0

  C．1

  D．-2
  组卷：130引用：3难度：0.8

  解析

• 3．已知

  96

  n

  是整数，正整数n的最小值为（　　）

  A．96

  B．6

  C．24

  D．2
  组卷：2853引用：11难度：0.5

  解析

• 4．下列计算错误的是（　　）

  A． 3 7 - 7 = 3

  B． 24 ÷ 2 = 2 3

  C． 25 a + 9 a = 8 a

  D． 14 × 7 = 7 2
  组卷：43引用：1难度：0.7

  解析

• 5．我国是最早了解勾股定理的国家之一，它被记载于我国古代著名的数学著作《周髀算经》中．下列各组数中，是“勾股数”的是（　　）

  A．2，3，4

  B．4，5，6

  C．7，8，9

  D．6，8，10
  组卷：694引用：17难度：0.7

  解析

• 6．若xy＜0，则

  x

  2

  y

  化简后的结果是（　　）

  A． x y

  B． x - y

  C． - x - y

  D． - x y
  组卷：2157引用：37难度：0.9

  解析

• 7．如图，▱ABCD的对角线AC，BD相交于点O，若AC+BD=20，CD=7，则△ABO的周长是（　　）

  A．16

  B．17

  C．20

  D．27
  组卷：100引用：3难度：0.6

  解析

• 8．矩形ABCD中，对角线AC，BD相交于点O，如果∠AOB=40°，那么∠ADB的度数是（　　）

  A．70°

  B．45°

  C．30°

  D．20°
  组卷：447引用：11难度：0.8

  解析

四、解答题（本大题共2小题，共20分。解答应写出文字说明，证明过程或演算步骤）

• 24．如图，在等边△ABC中，BC=6cm,射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）．
  （1）连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF；
  （2）①求当t为何值时，以A、F、C、E为顶点的四边形是平行四边形；
  ②求当t为何值时，四边形ACFE是菱形．
  组卷：275引用：5难度：0.4

  解析

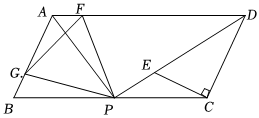• 25．如图，已知平行四边形ABCD，点P为BC的中点，连接PA，PD，PA⊥PD．
  （1）求证：DP平分∠ADC；
  （2）过点C作CE⊥CD交PD于点E，∠PCE=

  1

  2

  ∠B，PE=3

  3

  ，求▱ABCD的周长；
  （3）在（2）的条件下，点F为AD上一点，PF=8，G为AB上一点，∠FPG=60°，求△AGF的周长．
  组卷：227引用：4难度：0.4

  解析