2022-2023学年安徽省阜阳市临泉县鲖城中心学校九年级（上）期中数学试卷

一、选择题。（本大题共10小题，每小题4分，共40分）

• 1．如图，在△ABC中，点D在线段BC上，∠B=∠DAC，AC=8，BC=16，那么CD（　　）

  A．4

  B．6

  C．8

  D．10
  组卷：1409引用：8难度：0.5

  解析

• 2．在△ABC和△A₁B₁C₁中，下列命题中真命题的个数为（　　）
  （1）若∠A=∠A₁，∠C=∠C₁，则△ABC∽△A₁B₁C₁；
  （2）若AC：A₁C₁=CB：C₁B₁，∠C=∠C₁，则△ABC∽△A₁B₁C₁；
  （3）若AB=kA₁B₁，AC=kA₁C₁，（k≠0），∠A=∠A₁，则△ABC∽△A₁B₁C₁；
  （4）若S_△ABC=S

  △

  A

  1

  B

  1

  C

  1

  ，则△ABC∽△A₁B₁C₁．

  A．1

  B．2

  C．3

  D．4
  组卷：849引用：3难度：0.9

  解析

• 3．抛物线y=-（x-2）²+3的顶点坐标是（　　）

  A．（-2，3）

  B．（2，3）

  C．（2，-3）

  D．（-2，-3）
  组卷：720引用：22难度：0.9

  解析

• 4．已知

  b

  a

  =5，则

  a

  -

  b

  a

  +

  b

  的值是（　　）

  A． - 2 3

  B．- 1 3

  C． 2 3

  D． 1 3
  组卷：1127引用：9难度：0.7

  解析

• 5．若△ABC∽△A′B′C′，AB=2，A′B′=4，则△ABC与△A′B′C′的面积的比为（　　）

  A．1：2

  B．2：1

  C．1：4

  D．4：1
  组卷：429引用：7难度：0.9

  解析

• 6．已知点D、E分别在△ABC的边AB、AC上，下列给出的条件中，不能判定DE∥BC的是（　　）

  A．BD：AB=CE：AC	B．DE：BC=AB：AD
  C．AB：AC=AD：AE	D．AD：DB=AE：EC
  组卷：399引用：6难度：0.9

  解析

• 7．下面两个三角形一定相似的是（　　）

  A．两个等腰三角形	B．两个直角三角形
  C．两个钝角三角形	D．两个等边三角形
  组卷：202引用：38难度：0.9

  解析

• 8．抛物线y=2（x+3）²+1的顶点坐标是（　　）

  A．（3，1）

  B．（3，-1）

  C．（-3，1）

  D．（-3，-1）
  组卷：837引用：104难度：0.9

  解析

• 9．一次函数y₁=kx+b（k≠0）与反比例函数

  y

  2

  =

  m

  x

  （

  m

  ≠

  0

  ）

  ，在同一平面直角坐标系中的图象如图所示，若y₁＞y₂，则x的取值范围是（　　）

  A．-2＜x＜0或x＞1	B．x＜-2或0＜x＜1
  C．x＞1	D．-2＜x＜1
  组卷：51引用：15难度：0.9

  解析

• 10．如果抛物线y=（x+3）²+m与x轴的一个交点的坐标为（-1，0），那么另一个交点的坐标为（　　）

  A．（-6，0）

  B．（-5，0）

  C．（-4，0）

  D．（-3，0）
  组卷：63引用：1难度：0.9

  解析

二、填空题。（本大题共4个小题，每小题5分，满分20分）

• 11．如图，在△ABC中，D，E分别是AB，BC上的点，且DE∥AC，AE，CD交于点F，若S_△BDE：S_△DEC=1：3，则S_△DEF：S_△AFC=

   

  ．
  组卷：418引用：3难度：0.7

  解析

• 12．用总长为20m的围栏材料，一面靠墙，围成一个矩形花圃ABCD，如图所示．设AB的长为x m（0＜x＜10），矩形的面积为y m²，则y与x之间的函数关系式为

  ．
  组卷：199引用：2难度：0.6

  解析

• 13．反比例函数y=

  2

  -

  k

  x

  的图象经过点（-2，-3），则k的值为

  ．
  组卷：136引用：1难度：0.6

  解析

• 14．已知P是线段AB的黄金分割点，PA＞PB，AB=2cm,则PA=

  ．
  组卷：44引用：3难度：0.6

  解析

三、解答题。（本大题共2小题，每小题8分，满分16分）

• 15．如图，△ABC为一锐角三角形，BC=12，BC边上的高AD=8．点Q，M在边BC上，P，N分别在边AB，AC上，且PNMQ为矩形．
  （1）设MN=x,用x表示PN的长度；
  （2）当MN长度为多少时，矩形PNMQ的面积最大，最大面积是多少？
  （3）当MN长度为多少时，△APN的面积等于△BPQ与△CMN之和？
  组卷：620引用：2难度：0.5

  解析

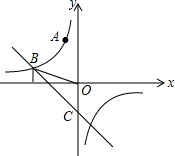• 16．如图，在平面直角坐标系中，一次函数y=kx+b的图象与反比例函数y=

  n

  x

  的图象交于点B（m,1），与y轴交于点C，且△BOC的面积为3，点A（-1，3）在反比例函数的图象上．求：
  （1）反比例函数的表达式；
  （2）直线BC的函数表达式．
  组卷：241引用：55难度：0.5

  解析

四、解答题。（本大题共2小题，每小题8分，满分16分）

• 17．如图①，正方形ABCD中，点A、B的坐标分别为（0，10）、（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．
  （1）当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；
  （2）求正方形边长及顶点C的坐标；
  （3）在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标．
  
  组卷：417引用：2难度：0.3

  解析

• 18．已知一个二次函数y=ax²+bx+c的图象如图所示，请求出这个二次函数的解析式．
  组卷：489引用：2难度：0.5

  解析

五、解答题。（本大题共2小题，每小题10分，满分20分）

• 19．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，1），B（-1，4），C（-3，2）．
  （1）画出△ABC关于y轴对称的图形△A₁B₁C₁，并直接写出C₁点坐标；
  （2）以原点O为位似中心，位似比为2：1，在y轴的左侧，画出△ABC放大后的图形△A₂B₂C₂，并直接写出C₂点坐标；
  （3）如果点D（a,b）在线段AB上，请直接写出经过（2）的变化后点D的对应点D₂的坐标．
  组卷：1857引用：59难度：0.5

  解析

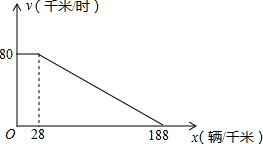• 20．“城市发展 交通先行”，成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程，建成后将大大提升二环路的通行能力．研究表明，某种情况下，高架桥上的车流速度V（单位：千米/时）是车流密度x（单位：辆/千米）的函数，且当0＜x≤28时，V=80；当28＜x≤188时，V是x的一次函数．函数关系如图所示．
  （1）求当28＜x≤188时，V关于x的函数表达式；
  （2）若车流速度V不低于50千米/时，求当车流密度x为多少时，车流量P（单位：辆/时）达到最大，并求出这一最大值．
  （注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量=车流速度×车流密度）
  组卷：845引用：12难度：0.3

  解析

六、解答题。（本题满分12分）

• 21．如图，一农户要建一个矩形鸡舍，为了节省材料鸡舍的一边利用墙，另外三边用长为27米的建筑材料围成，为方便进出，在垂直墙的一边留下一个宽1米的门．设AB=x米时，鸡舍面积为S平方米．
  （1）求S关于x的函数表达式及x的取值范围．
  （2）在（1）的条件下，当AB为多少时，鸡舍的面积为90平方米？
  （3）若住房墙的长度足够长，问鸡舍面积能否达到100平方米？
  组卷：630引用：3难度：0.6

  解析

七、解答题。（本题满分12分）

• 22．如图，在平面直角坐标系中，已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动；点Q从点B开始沿BO边向点O以1cm/s的速度移动，如果P，Q同时出发，用t（s）表示移动的时间（0≤t＜6），那么：
  （1）设△POQ的面积为y,求y关于t的函数解析式．
  （2）当△POQ的面积为4.5cm²时，△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由．
  （3）当t为何值时，△POQ与△AOB相似．
  组卷：81引用：2难度：0.2

  解析

八、解答题（本题满分14分）

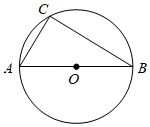• 23．如图，△ABC内接于⊙O，∠ACB=90°．
  （1）利用尺规，作∠ACB的平分线交⊙O于点D（保留作图痕迹，不写作法）；
  （2）在（1）的条件下，连接OD、AD、CD，CD交AB于点E．
  ①若∠BAC=60°，求∠ODC的度数；
  ②求证：AD²=DE•DC．
  组卷：119引用：2难度：0.5

  解析