2022-2023学年广东省东莞中学松山湖学校九年级（上）期中数学试卷

一、选择题：本题共10小题，每小题3分，共30分.

• 1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：66引用：3难度：0.8

  解析

• 2．一元二次方程x²+3x=0的解是（　　）

  A．x=-3

  B．x1=0，x2=3

  C．x1=0，x2=-3

  D．x=3
  组卷：622引用：72难度：0.9

  解析

• 3．抛物线y=3（x-1）²-1的顶点坐标是（　　）

  A．（1，1）

  B．（-1，1）

  C．（-1，-1）

  D．（1，-1）
  组卷：278引用：6难度：0.6

  解析

• 4．一元二次方程2x²-4x+3=0的根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．没有实数根	D．无法确定
  组卷：159引用：5难度：0.6

  解析

• 5．已知△ABC∼△DEF，且△ABC的面积为2cm²，△DEF的面积为8cm²，则△ABC与△DEF的相似比是（　　）

  A．1：4

  B．4：1

  C．1：2

  D．2：1
  组卷：493引用：2难度：0.7

  解析

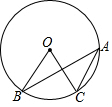• 6．如图，点A，B，C在⊙O上，若∠BOC=72°，则∠BAC的度数是（　　）

  A．18°

  B．36°

  C．54°

  D．72°
  组卷：708引用：12难度：0.8

  解析

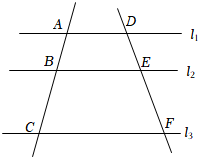• 7．如图，直线l₁∥l₂∥l₃，直线AC和DF被l₁、l₂、l₃所截，AB=6，BC=8，DE=4，则EF的长为（　　）

  A．12

  B．3

  C． 16 3

  D．5
  组卷：283引用：2难度：0.5

  解析

五、解答题（三）：本小题共2小题，每小题12分，共24分.

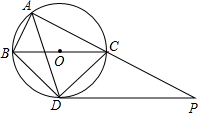• 22．如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．
  （1）求证：PD是⊙O的切线；
  （2）求证：△ABD∽△DCP；
  （3）当AB=5cm,AC=12cm时，求线段PC的长．
  组卷：3848引用：24难度：0.1

  解析

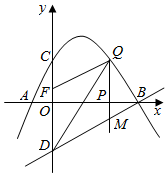• 23．如图，已知抛物线y=ax²+bx+2经过点A（-1，0），B（4，0），点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m,0），过点P作x轴的垂线l交抛物线于点Q，交BD所在直线于点M．
  （1）求该抛物线所表示的二次函数的表达式；
  （2）已知点F（0，

  1

  2

  ），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？
  （3）点P在线段AB上运动过程中，是否存在点Q，使得以点B，Q，M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由．
  组卷：529引用：3难度：0.3

  解析