2022-2023学年重庆市南川区九年级（上）期末数学试卷

一、选择题（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

• 1．点（3，-2）关于原点对称的点的坐标为（　　）

  A．（-3，2）

  B．（-3，-2）

  C．（3，2）

  D．（-2，3）
  组卷：226引用：6难度：0.8

  解析

• 2．下列事件为必然事件的是（　　）

  A．太阳从东方升起

  B．射击运动员射击一次，命中靶心

  C．购买一张彩票中奖一百万元

  D．篮球队员在罚球线上投篮一次，未投中
  组卷：43引用：2难度：0.9

  解析

• 3．抛物线y=3（x+2）²-1的顶点坐标是（　　）

  A．（2，-1）

  B．（2，1）

  C．（-2，1）

  D．（-2，-1）
  组卷：168引用：3难度：0.7

  解析

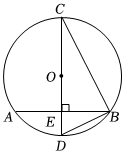• 4．如图，CD是⊙O的直径，弦AB⊥CD于E，连接BC、BD，下列结论中不一定正确的是（　　）

  A．AE=BE

  B． ˆ AD = ˆ BD

  C．OE=DE

  D．∠DBC=90°
  组卷：1125引用：83难度：0.7

  解析

• 5．一个布袋里装有8个只有颜色不同的球，其中2个红球，6个白球．从布袋里任意摸出1个球，则摸出的球是白球的概率为（　　）

  A． 3 4

  B． 1 4

  C． 1 3

  D． 1 5
  组卷：46引用：2难度：0.7

  解析

• 6．一元二次方程x²-2x+3=0的根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．只有一个实数根	D．没有实数根
  组卷：200引用：5难度：0.6

  解析

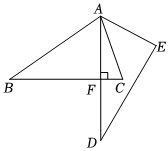• 7．如图，将△ABC绕点A逆时针旋转50°得到△ADE，若∠E=70°且AD⊥BC于点F，则∠BAC的度数为（　　）

  A．65°

  B．70°

  C．75°

  D．80°
  组卷：589引用：10难度：0.7

  解析

• 8．已知点A（-2，y₁），B（1，y₂），C（3，y₃），都在函数

  y

  =

  3

  x

  的图象上，则y₁、y₂、y₃的大小关系是（　　）

  A．y1＞y3＞y2

  B．y1＞y2＞y3

  C．y2＞y1＞y3

  D．y2＞y3＞y1
  组卷：224引用：4难度：0.7

  解析

四、解答题（本题7个小题，每小题10分，共70分）解答时必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

• 24．如图1，在平面直角坐标系中，二次函数y=ax²+bx-3（a≠0）的图象与x轴于A（-1，0），B（3，0）两点，与y轴交于C点，点P是直线BC下方抛物线上一动点．
  
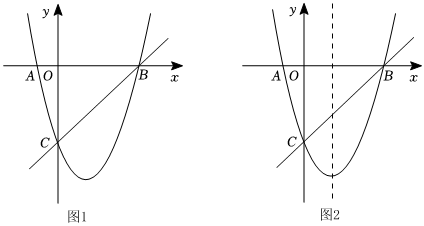
  （1）求这个二次函数的解析式；
  （2）当动点P运动到什么位置时，使四边形ACPB的面积最大，求出此时四边形ACPB的面积最大值和P的坐标；
  （3）如图2，点M在抛物线对称轴上，点N是平面内一点，是否存在这样的点M、N，使得以点M、N、A、C为顶点的四边形是菱形？若存在，请直接写出所有M点的坐标；若不存在，请说明理由．
  组卷：1185引用：4难度：0.6

  解析

• 25．如图1，在正方形ABCD中，对角线AC、BD相交于点O，点E为线段BO上一点，连接CE，将CE绕点C顺时针旋转90°得到CF，连接EF交CD于点G．
  
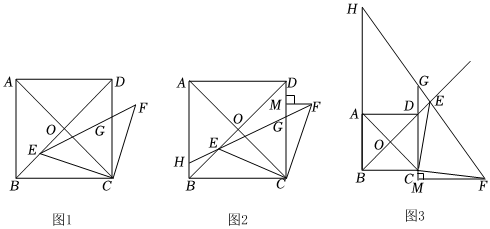
  （1）若AB=8，BE=2

  2

  ，求△CEF的面积．
  （2）如图2，线段FE的延长线交AB于点H，过点F作FM⊥CD于点M，求证：BH+MG=

  2

  2

  BE；
  （3）如图3，点E为射线OD上一点，线段FE的延长线交直线CD于点G，交直线AB于点H，过点F作FM垂直直线CD于点M，请直接写出线段BH、MG、BE的数量关系．
  组卷：337引用：2难度：0.1

  解析