当前位置：试卷中心 > 试卷详情

2022年黑龙江省哈尔滨市南岗区松雷中学中考数学模拟试卷（6月份）

发布：2025/11/14 6:0:11

一、选择题（每小题3分，共计30分）

1．在平面直角坐标系中，反比例函数y=
a
2
-
a
+
2
x
图象的两个分支分别在（　　）
A．第一、三象限 B．第二、四象限
C．第一、二象限 D．第三、四象限
组卷：312引用：6难度：0.9
2．下列运算正确的是（　　）
A．3a-a=2 B．（a²）³=a⁵ C．a²•a³=a⁵ D．a⁶÷a³=a²
组卷：265引用：9难度：0.9
3．a（a≠0）的相反数是（　　）
A．-a B．a² C．|a| D．
1
a
组卷：644引用：56难度：0.9
4．抛物线y=3x²向右平移2个单位，再向下平移3个单位，所得到的抛物线是（　　）
A．y=3（x-2）²-3 B．y=3（x+2）²-3
C．y=3（x+2）²+3 D．y=3（x-2）²+3
组卷：99引用：5难度：0.6
5．下列图形中，是轴对称图形但不是中心对称图形的是（　　）
A． B． C． D．
组卷：186引用：10难度：0.7
6．在Rt△ABC中，∠C=90°，若△ABC的三边都扩大3倍，则sinA的值（　　）
A．放大3倍 B．缩小3倍 C．不变 D．无法确定
组卷：427引用：3难度：0.7
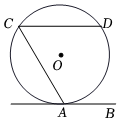7．如图，直线AB与⊙O相切于点A，AC、CD是⊙O的两条弦，且CD∥AB，若⊙O的半径为5，CD=8，则弦AC的长为（　　）
A．4
5
B．4
3
C．4
2
D．4
10
组卷：678引用：4难度：0.6
8．下列几何体中，主视图是长方形的是（　　）
A． B． C． D．
组卷：579引用：10难度：0.9
9．分式方程
3
x
-
2
x
-
2
=0的解为（　　）
A．x=6 B．x=-6 C．x=2 D．原方程无解
组卷：41引用：2难度：0.9
10．如图，在▱ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为（　　）
A．
16
3
B．8 C．10 D．16
组卷：1509引用：33难度：0.9

二、填空题（每小题3分，共计30分）

11．一台空调标价2000元，若按7折销售仍可获利40%，则这台空调的进价是
元．
组卷：590引用：5难度：0.6
12．不等式组
3
x
-
1
＞
2
x
-
（
x
-
4
）
≥
-
2
的解集是
．
组卷：221引用：1难度：0.5
13．阜建高速公路的建设批复总投资213000万元，用科学记数法表示总投资为
万元．
组卷：34引用：1难度：0.7
14．函数y=
x
-
1
2
的自变量x的取值范围是

．
组卷：191引用：17难度：0.7
15．已知扇形的弧长为4π，半径为36，则此扇形的圆心角为
度．
组卷：243引用：2难度：0.8
16．抛物线
y
=
-
1
2
x
2
-
2
，当x=
时，函数取得最
值．
组卷：132引用：2难度：0.8
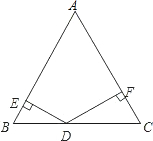17．如图，△ABC是等边三角形，点D是BC边上任意一点，DE⊥AB于点E，DF⊥AC于点F．若BC=2，则DE+DF=

．
组卷：887引用：34难度：0.7
18．若矩形一个内角的角平分线把矩形的另一条边分为4cm、5cm两部分，则这个矩形的周长是

．
组卷：110引用：2难度：0.7
19．计算：
12
+
27
=
．
组卷：2430引用：48难度：0.7
20．分解因式：3m²-27=
．
组卷：1001引用：132难度：0.7

三、解答题：（21、22题各7分，23、24题各8分，25-27题各10分，共计60分）

21．“校园手机”现象越来越受到社会的关注，为此某媒体记者小李随机调查了某校若干名中学生家长对这种现象的态度（态度分为：A：无所谓；B：反对；C：赞成），并将调查结果绘制成图①和图②的统计图（不完整），请根据图中提供的信息，解答下列问题：

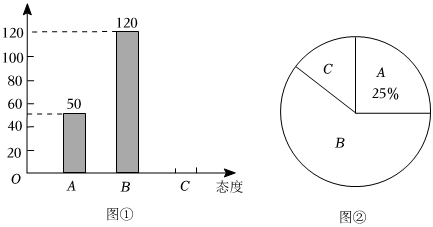
（1）此次抽样调查中，共调查了
名中学生家长，图②中表示家长“赞成”的圆心角的度数为
；
（2）将图①补充完整；
（3）根据抽样调查结果，请你估计该校2100名中学生家长中有多少名家长持反对态度．
组卷：4引用：1难度：0.6
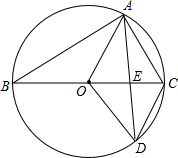22．如图所示，已知BC是⊙O的直径，A、D是⊙O上的两点．
（1）若∠ACB=58°，求∠ADC的度数；
（2）当
ˆ
CD
=
1
2
ˆ
AC
时，连接CD、AD，其中AD与直径BC相交于点E，求证：2CD²=CE•BC；
（3）在（2）的条件下，若∠COD=45°，CE=
2
，求
BC
•
CE
AB
的值．
组卷：233引用：3难度：0.5
23．已知：AC是平行四边形ABCD的对角线，且BE⊥AC，DF⊥AC，连接DE、BF．
求证：四边形BFDE是平行四边形．
组卷：623引用：4难度：0.4
24．某足球特色学校在商场购买甲、乙两种品牌的足球．已知乙种足球比甲种足球每只贵20元，该校分别花费2000元、1400元购买甲、乙两种足球，这样购得甲种足球的数量是购得乙种足球数量的2倍，求甲、乙两种足球的单价各是多少元？
组卷：386引用：4难度：0.1
25．先化简，再求值：
（
x
-
1
x
-
2
+
2
x
-
8
x
2
-
4
）
÷
（
x
+
5
）
，其中
x
=
3
-
2
．
组卷：120引用：2难度：0.7
26．如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，OA=1，
OB
=
3
OA
，直线
OC
：
y
=
3
x
交直线AB于点C．

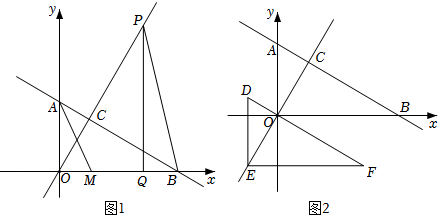
（1）求直线AB的解析式及C点的坐标；
（2）如图1，P为直线OC上一动点且在第一象限内，M、Q为x轴上动点，Q在M右侧且
MQ
=
3
2
，当
S
△
PCB
=
9
3
8
时，求PQ+QM+MA最小值；
（3）如图2，将△AOB沿着射线CO方向平移，平移后A、O、B三点分别对应D、E、F三点，当DF过O点时，在平面内是否存在H点，在第一象限内是否存在N点，使得以H、N、D、F四个点为顶点的四边形为正方形，若存在，请直接写出H点坐标；若不存在，请说明理由．
组卷：1540引用：7难度：0.3
27．图1，图2，均为正方形网格，每个小正方形的面积均为1．在这个正方形网格中，各个小正方形的顶点叫做格点．请在下面的网格中按要求画图，使得每个图形的顶点均在格点上．
（1）画一个直角三角形，且三边之比为1：2：
5
；
（2）画一个边长为整数的菱形，且面积等于20．
组卷：36引用：5难度：0.5