2022-2023学年浙江省湖州市安吉二中九年级（上）第一次测试数学试卷

一、选择题（40分）

• 1．二次函数y=x²+4x+5与坐标轴的交点个数是（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：51引用：2难度：0.7

  解析

• 2．若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数，如796就是一个“中高数”．若十位上数字为7，则从3、4、5、6、8、9中任选两数，与7组成“中高数”的概率是（　　）

  A． 1 2

  B． 2 3

  C． 2 5

  D． 3 5
  组卷：1451引用：68难度：0.9

  解析

• 3．观察数列：1，2，5，12，29，70，169，□，…的规律性，则根据上述规律，□所表示的数应是（　　）

  A．239

  B．250

  C．389

  D．408
  组卷：13引用：1难度：0.5

  解析

• 4．如图，已知P是正方形ABCD内一点，△PBC是等边三角形，若△PAD的外接圆半径为a,则正方形ABCD边长为（

  A． 1 2 a

  B． 3 2 a

  C．a

  D． 2 a
  组卷：213引用：2难度：0.7

  解析

• 5．如图，在半径为

  13

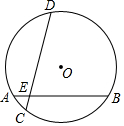  的⊙O中，弦AB与CD交于点E，∠DEB=75°，AB=6，AE=1，则CD的长是（　　）

  A．2 6

  B．2 10

  C．2 11

  D．4 3
  组卷：12135引用：31难度：0.5

  解析

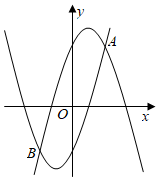• 6．如图，抛物线y₁=a（x+1）²-5与抛物线y₂=-a（x-1）²+5（a≠0）交于点A（2，4），B（m,-4），若无论x取任何值，y总取y₁，y₂中的最小值，则y的最大值是（　　）

  A．4

  B．5

  C．2

  D．1
  组卷：1567引用：4难度：0.5

  解析

三、解答题（50分）

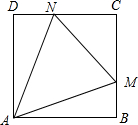• 17．已知正方形ABCD的边长为1，点M、N分别是边BC、CD的两点，若△CMN的周长为2，求：
  （1）∠MAN的大小；
  （2）△AMN面积的最小值．
  组卷：251引用：2难度：0.4

  解析

• 18．直线y=-x+3与x轴相交于点A，与y轴相交于点B，抛物线y=ax²+2x+c经过点A，B，与x轴的另一个交点为C．
  （1）求抛物线的解析式；
  （2）如图1，点D是第一象限内抛物线上的一个动点，过点D作DE∥y轴交AB于点E，DF⊥AB于点F，FG⊥x轴于点G．当DE=FG时，求点D的坐标；
  （3）如图2，在（2）的条件下，直线CD与AB相交于点M，点H在抛物线上，过H作HK∥y轴，交直线CD于点K．P是平面内一点，当以点M，H，K，P为顶点的四边形是正方形时，请直接写出点P的坐标．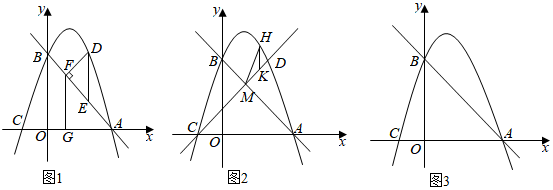
  
  组卷：2588引用：5难度：0.2

  解析