当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省盐城市东台市第五教育联盟九年级（下）期中数学试卷

发布：2024/7/26 8:0:9

一、选择题（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

1．-2023的相反数等于（　　）
A．-2023 B．2023 C．±2023 D．
1
2023
组卷：324引用：17难度：0.7
解析
2．下列图案中，是轴对称图形的是（　　）
A． B． C． D．
组卷：562引用：22难度：0.9
解析
3．将141260用科学记数法可表示为（　　）
A．0.14126×10⁶ B．1.4126×10⁶
C．1.4126×10⁵ D．14.126×10⁴
组卷：35引用：1难度：0.8
解析
4．如图，已知∠1=90°，为保证两条铁轨平行，添加的下列条件中，正确的是（　　）
A．∠2=90° B．∠3=90° C．∠4=90° D．∠5=90°
组卷：1209引用：28难度：0.6
解析
5．下列事件是必然事件的是（　　）
A．三角形内角和是180°
B．端午节赛龙舟，红队获得冠军
C．掷一枚均匀骰子，点数是6的一面朝上
D．打开电视，正在播放神舟十四号载人飞船发射实况
组卷：924引用：21难度：0.7
解析
6．已知一组数据：23，22，24，23，23，这组数据的方差是（　　）
A．3 B．2 C．
3
5
D．
2
5
组卷：412引用：5难度：0.7
解析
7．在Rt△ABC中，∠C=90°，tanA=
5
12
，则cosA等于（　　）
A．
5
12
B．
12
5
C．
5
13
D．
12
13
组卷：2292引用：24难度：0.7
解析
8．某项工作，已知每人每天完成的工作量相同，且一个人完成需12天．若m个人共同完成需n天，选取6组数对（m,n），在坐标系中进行描点，则正确的是（　　）
A． B．
C． D．
组卷：1659引用：16难度：0.5
解析

二、填空题（本大题共8小题，每小题3分，共24分，其不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）

9．计算：a³•a⁴=

．
组卷：1096引用：7难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共11小题，共102分，请在答题卡指定区城内作答，解答时应写出文字说明、证明过程或演算步骤）

26．【定义】在平面内，把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值，称为这两个图形之间的距离，即A、B分别是图形M和图形N上任意一点，当AB的长最小时，称这个最小值为图形M与图形N之间的距离．
例如，如图1，AB⊥l₂，线段AB的长度称为点A与直线l₂之间的距离，当l₂∥l₁时，线段AB的长度也是l₁与l₂之间的距离．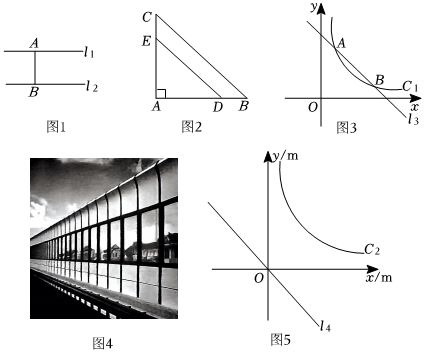

【应用】：
（1）如图2，在等腰直角三角形BAC中，∠A=90°，AB=AC，点D为AB边上一点，过点D作DE∥BC交AC于点E．若AB=12，AD=8，则DE与BC之间的距离是
．
（2）如图3，已知直线l₃：y=-x+8与双曲线C₁：y=
k
x
（x＞0）交于A（2，m）与B两点，点A与点B之间的距离是
，点O与双曲线C₁之间的距离是
；
【拓展】：
（3）按规定，住宅小区的外延到高架路的距离不超过80m时，需要在高架路旁修建与高架路相同走向的隔音屏障（如图4）．有一条“东南-西北”走向的笔直高架路，路旁某住宅小区建筑外延呈双曲线的形状，它们之间的距离小于80m.现以高架路上某一合适位置为坐标原点，建立如图5所示的平面直角坐标系，此时高架路所在直线l₄的函数表达式为y=-x,小区外延所在双曲线C₂的函数表达式为y=
3000
x
（x＞0），那么需要在高架路旁修建隔音屏障的长度是多少？
组卷：538引用：3难度：0.2
解析
27．如图①，在矩形ABCD中，点P从AB边的中点E出发，沿着E-B-C匀速运动，速度为每秒2个单位长度，到达点C后停止运动，点Q是AD上的点，AQ=10，设△APQ的面积为y,点P运动的时间为t秒，y与t的函数关系如图②所示．
（1）图①中AB=
，BC=
，图②中m=
；
（2）当t=1秒时，试判断以PQ为直径的圆是否与BC边相切？请说明理由；
（3）点P在运动过程中，将矩形沿PQ所在直线折叠，则t为何值时，折叠后顶点A的对应点A′落在矩形的一边上．
组卷：882引用：3难度：0.1
解析