2022-2023学年广西南宁十三中九年级（上）第三次月考数学试卷

一、选择题（共36分）

• 1．下列图形是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：98引用：4难度：0.7

  解析

• 2．2020年国庆中秋假日期间，广西共接待游客超32550000人次，按可比口径同比恢复85.6%，实现旅游消费接近224亿元，按可比口径同比恢复85.9%．数据32550000用科学记数法表示为（　　）

  A．3255×104

  B．3.255×107

  C．3.255×104

  D．32.55×106
  组卷：2引用：3难度：0.9

  解析

• 3．如图点O为数轴的原点，若点A表示的数是a,点B表示的数是b,那么下列关系正确的是（　　）

  A．a＞0

  B．b＜0

  C．a＜b

  D．a＞b
  组卷：6引用：3难度：0.8

  解析

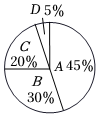• 4．某高中饭堂为了了解学生对四种早餐套餐的喜爱程度，随机抽取在校200名学生进行最爱最喜爱早餐套餐的调查（每人选一种），绘制了如图的扇形统计图．根据图中的信息，学生最喜欢的套餐种类是（　　）

  A．套餐A

  B．套餐B

  C．套餐C

  D．套餐D
  组卷：10引用：6难度：0.8

  解析

• 5．下列计算正确的是（　　）

  A．3x2+2x2=5x4	B．x3•x3=2x3
  C．（x4）3=x7	D．10ab3÷（-5ab）=-2b2
  组卷：13引用：3难度：0.7

  解析

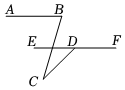• 6．如图，AB∥EF，∠ABC=80°，∠CDF=135°，则∠BCD的度数为（　　）

  A．30°

  B．35°

  C．55°

  D．80°
  组卷：15引用：4难度：0.6

  解析

• 7．“漏壶”是古代一种计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度．人们根据壶中水面的位置计算时间．在漏壶漏完水之前，漏壶内水的深度与对应的漏水时间满足的函数关系式（　　）

  A．正比例函数关系	B．一次函数关系
  C．反比例函数关系	D．二次函数关系
  组卷：75引用：4难度：0.6

  解析

• 8．一个不透明布袋里共有4个球（只有编号不同），编号分别为1，2，3，5，从中任意摸出一个球，记下编号后放回，搅匀，再任意摸出一个球，则两次摸出的球的编号之和为偶数的概率是（　　）

  A． 5 8

  B． 1 2

  C． 3 8

  D． 1 4
  组卷：10引用：1难度：0.5

  解析

三、解答题（共66分）

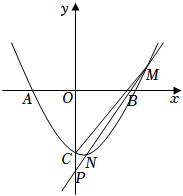• 25．如图，抛物线经过A（-2，0），C（0，-3）两点，且对称轴为直线

  x

  =

  1

  2

  ．
  （1）求抛物线的函数解析式；
  （2）若直线y=kx-5与抛物线交于点M，N，交x轴于点B，交y轴于点P，连接CN，且

  tan

  ∠

  OPM

  =

  1

  2

  ．
  ①求△CMN的面积；
  ②在平面内是否存在点一是E，使E，C，N，M四点能构成平行四边形，如果存在，请直接写出点E的坐标．
  组卷：10引用：3难度：0.3

  解析

• 26．如图，已知AC为⊙O的直径，连接AB，BC，OB，过点O作OE⊥AB于点E，点F是半径OC的中点，连接EF，BF．
  （1）如图1，设⊙O的半径为2，若∠BAC=30°，求线段EF的长．
  （2）如图2，设BO交EF于点P，延长BO交⊙O于点D，连接DF．
  ①求证：PE=PF；
  ②若DF=EF，求∠BAC的度数．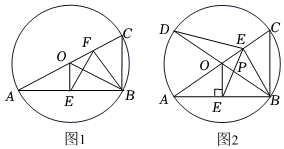
  
  组卷：115引用：4难度：0.2

  解析