2022-2023学年湖北省武汉市武昌区水果湖一中九年级(上)期中数学试卷
发布:2024/9/29 21:0:2
一、选择题(本大题共10小题,共30.0分.在每小题列出的选项中,选出符合题目的一项)
-
1.下列方程为一元二次方程的是( )
组卷:32引用:4难度:0.8 -
2.如所示图形中,既是轴对称图形,又是中心对称图形的是( )
组卷:146引用:6难度:0.8 -
3.抛物线y=
(x-6)2+3的顶点坐标为( )12组卷:120引用:4难度:0.9 -
4.关于x的方程x2-4x+m+2=0有一个根为-1,则另一个根为( )
组卷:1004引用:17难度:0.6 -
5.下列说法正确的是( )
组卷:41引用:3难度:0.7 -
6.将抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
组卷:204引用:9难度:0.9 -
7.某品牌服装,经过两次调价,从每件1000元降至810元,则该服装平均每次降价率为( )
组卷:566引用:2难度:0.5 -
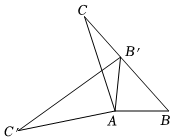 8.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为( )组卷:4721引用:55难度:0.7
8.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为( )组卷:4721引用:55难度:0.7
三、解答题(本大题共8小题,共72.0分.解答应写出文字说明,证明过程或演算步骤)
-
23.如图1,△ABC中,AB=AC,∠BAC=α,点D、E分别在AB、AC上,AD=AE.将△ADE绕点A逆时针旋转β(0°<β<360°),使得B、D、E三点共线.
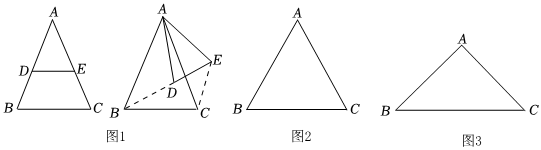
(1)直接写出:∠ADB=(用α表示);
(2)若α=60°,当0°<β<360°时,作AF⊥DE于F,在图2中画出符合要求的图形,并探究BE、CE、AF之间的数量关系,并证明你的结论;
(3)如图3,若α=90°,,当0<β<180时,直接写出S四边形ABCE的最大值.AC=82组卷:208引用:4难度:0.3 -
24.已知抛物线的顶点H(2,0),经过点A(1,1),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;
(3)如图2,过点P(-3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PM•PN的值.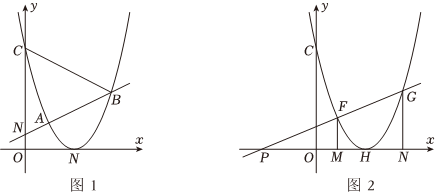 组卷:514引用:3难度:0.4
组卷:514引用:3难度:0.4


