2021-2022学年江西省吉安市井冈山市八年级(下)期末数学试卷
发布:2024/7/11 8:0:9
一、选择题(本大题共6小题,每小题3分,共18分)
-
1.保护环境,人人有责.下列四个图形是生活中常见的垃圾回收标志,是中心对称图形的是( )
组卷:392引用:10难度:0.9 -
2.下列式子①x>0;②
;③2x<-2+x;④x+y>-3;⑤x=-1.其中是一元一次不等式的有( )1x<-1组卷:527引用:6难度:0.8 -
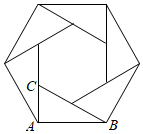 3.如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC等于( )组卷:1506引用:11难度:0.5
3.如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC等于( )组卷:1506引用:11难度:0.5 -
4.若关于x的方程
+x+mx-3=3的解为正数,则m的取值范围是( )3m3-x组卷:7362引用:63难度:0.7 -
5.随着市场对新冠疫苗需求越来越大,为满足市场需求,某大型疫苗生产企业更新技术后,加快了生产速度,现在平均每天比更新技术前多生产10万份疫苗,现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间相同,设更新技术前每天生产x万份,依据题意得( )
组卷:1508引用:15难度:0.6 -
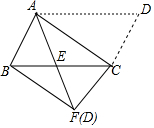 6.如图,将▱ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )组卷:494引用:5难度:0.7
6.如图,将▱ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )组卷:494引用:5难度:0.7
二、填空题(共6小题,每小题3分,共18分
-
7.将3x2y-27y因式分解为.
组卷:704引用:9难度:0.7
五、解答题(本大题共2小题,每小题9分,共18分)
-
22.文山学校梁老师在给他的学生上课时发现:
对折长方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM,把纸片展平,连接AN,如图①.
(1)折痕BM (填“是”或“不是”)线段AN的垂直平分线;请判断图中△ABN是什么特殊三角形?答:;进一步计算出∠MNE=°.
(2)继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,则∠GBN=°;
拓展延伸:
(3)如图③,折叠矩形纸片ABCD,使点A落在BC边上的点A′处,并且折痕交BC边于点T,交AD边于点S,把纸片展平,连接AA′交ST于点O,连接AT.
求证:四边形SATA′是平行四边形.
(4)如图④,矩形纸片ABCD中,AB=10,AD=26,折叠纸片,使点A落在BC边上的点A′处,并且折痕交AB边于点T,交AD边于点S,把纸片展平.同学们小组讨论后,得出线段AT的长度有4,5,7,9.
请写出以上4个数值中你认为正确的数值 .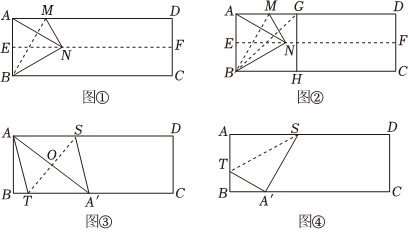 组卷:48引用:1难度:0.5
组卷:48引用:1难度:0.5
六、解答题(本大题共1小题,共12分
-
23.△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E.DF与线段AC(或AC的延长线)相交于点F.
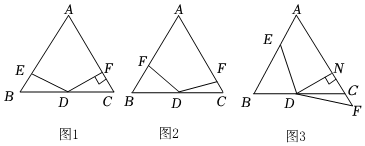
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:;BE+CF=12AB
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN=FN,求证:(BE+CF)2+(BE-CF)2=AB2.组卷:121引用:2难度:0.3


