2023年陕西省商洛市商南县湘河初级中学中考数学模拟试卷（三）

一、选择题（共8小题，每小题3分，计24分，每小题只有一个选项是符合题意的）

• 1．计算：（-2）+3=（　　）

  A．1

  B．-1

  C．5

  D．-5
  组卷：372引用：2难度：0.9

  解析

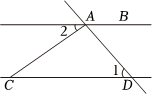• 2．如图，AB∥CD，若∠1=50°，∠2=35°，则∠CAD=（　　）

  A．85°

  B．90°

  C．95°

  D．105°
  组卷：57引用：1难度：0.8

  解析

• 3．计算（-3ab³）²的结果为（　　）

  A．-6a2b6

  B．-6ab6

  C．9a2b9

  D．9a2b6
  组卷：99引用：1难度：0.9

  解析

• 4．在▱ABCD中，添加下列条件，能判定▱ABCD是菱形的是（　　）

  A．AB=CD

  B．AC=BD

  C．AC⊥BD

  D．AB=AC
  组卷：285引用：5难度：0.6

  解析

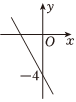• 5．如图，一次函数y=-2x+b的图象与y轴交于点（0，-4），当-4＜y＜0时，自变量x的取值范围是（　　）

  A．x＜-2

  B．-2＜x＜0

  C．0＜x＜2

  D．-4＜x＜0
  组卷：209引用：1难度：0.7

  解析

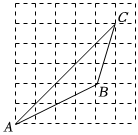• 6．如图，△ABC的顶点在正方形网格的格点上，则tanA的值为（　　）

  A． 1 3

  B． 1 2

  C． 5 5

  D． 3 3
  组卷：523引用：4难度：0.5

  解析

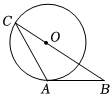• 7．如图，AB为⊙O的切线，A为切点，BO的延长线交⊙O于点C，若∠B的度数是36°，则∠C的度数是（　　）

  A．18°

  B．24°

  C．25°

  D．27°
  组卷：141引用：1难度：0.7

  解析

• 8．已知点P（2-m,n），Q（m+2，n），且m≠0，在抛物线L：y=ax²-（5-a）x+1+a上，则抛物线L与坐标轴的交点个数为（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：232引用：2难度：0.5

  解析

三、解答题（共13小题，计81分，解答应写出过程）

• 25．过原点的抛物线C：y=ax²+2ax（a＜0）与x轴的另一个交点为A，顶点为D．
  （1）求点A的坐标．
  （2）M（m,0）为x轴正半轴上一点，记抛物线C关于点M中心对称的抛物线C′，设抛物线C′与x轴的交点为E，F，点E在点F的左侧，抛物线C′的顶点为G．
  ①当m=1时，求点E与点F的坐标
  ②在①的条件下，当S_{四边形ADFG}=12时，求抛物线C′的表达式．
  组卷：66引用：1难度：0.5

  解析

• 26．问题提出
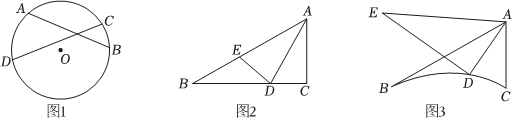
  （1）如图1，在半径为3的⊙O中，AB，CD为弦，则AB+CD的最大值为

  ．
  问题探究
  （2）如图2，在Rt△ABC中，∠C=90°，∠B=30°，AC=1，D为BC上任意一点，E为AB上任意一点，连接AD，DE，求AD+DE的最小值．
  问题解法
  （3）如图3，某同学运用电脑编程设计了一款游戏，在一个“曲边△ABC”中，AB，AC为线段，∠BAC=60°，BC为一段弧线，

  ˆ

  BC

  所在的圆与AB相切，D为

  ˆ

  BC

  上一点，一只电子蚂蚁从点A出发，其爬行路径为折线AD-DE，其中AD⊥DE，在DE段爬行的过程中，当时，电子蚂蚁停止移动．已知

  ˆ

  BC

  所在圆的半径为6，

  ˆ

  BC

  的长度为2π．结合题意，问当电子蚂蚁停止爬行时，线段AE是否存在最小距离？若存在，求出AE的最小距离；若不存在，请说明理由．
  ​
  组卷：110引用：1难度：0.5

  解析