2022-2023学年浙江省金华市东阳市江北中学等四校八年级（下）期中数学试卷

一、选择题（本题有10小题，每小题3分，共30分）

• 1．下列方程中，是一元二次方程的是（　　）

  A．x-9=0

  B．x2+6x+5=0

  C．y=x2-1

  D．x2-2x-3
  组卷：278引用：9难度：0.9

  解析

• 2．中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，如图四幅作品分别代表“立春”，“立夏”“芒种”“大雪”，其中既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1136引用：48难度：0.8

  解析

• 3．若式子

  4

  -

  2

  x

  在实数范围内有意义，则x的取值范围是（　　）

  A．x≥2

  B．x＞2

  C．x＜2

  D．x≤2
  组卷：424引用：5难度：0.7

  解析

• 4．2022年卡塔尔世界杯是第二十二届世界杯足球赛，是历史上首次在中东国家境内举行，也是第二次在亚洲举行的世界杯足球赛．如表是球迷小彬最喜欢的6支球队在本届世界杯中的总进球数（个），其中的中位数和众数分别是（　　）
  

  球队	西班牙	英格兰	巴西	阿根廷	法国	克罗地亚
  总进球数	9	13	8	15	16	8

  A．8个，8个

  B．11个，15个

  C．13个，15个

  D．11个，8个
  组卷：184引用：4难度：0.7

  解析

• 5．下列图形中，一定可以拼成平行四边形的是（　　）

  A．两个等腰三角形	B．两个全等三角形
  C．两个锐角三角形	D．两个直角三角形
  组卷：912引用：11难度：0.7

  解析

• 6．若要运用反证法证明“若a＞b＞0，则

  a

  ＜

  b

  ”，首先应该假设（　　）

  A． a ≥ b

  B． a ＞ b

  C． a ≤ b

  D． a ＜ b
  组卷：147引用：4难度：0.6

  解析

• 7．已知方程x²-2x-2=0的一个根是m,则代数式3m²-6m+2017的值为（　　）

  A．2022

  B．2023

  C．2024

  D．2025
  组卷：354引用：3难度：0.6

  解析

• 8．如图，在Rt△ABC中，∠B=90°，BC=4，AC=5，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是（　　）

  A．3

  B．6

  C．8

  D．10
  组卷：1290引用：5难度：0.6

  解析

三、解答题（共题共8小题，共66分，各小题都必须写出解答过程）

• 23．配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．我们定义：一个整数能表示成a²+b²（a、b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为5=2²+1².所以5是“完美数”．
  解决问题：
  （1）已知10是“完美数”，请将它写成a²+b²（a、b是整数）的形式

  ；
  （2）若x²-4x+3可配方成（x-m）²+n（m、n为常数），则mn=

  ；
  探究问题：
  （3）已知x²+y²-2x+6y+10=0，则x+y=

  ；
  （4）已知S=x²+9y²+4x-12y+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．
  拓展结论：
  （5）已知实数x、y满足-x²+

  7

  3

  x+y-2=0，求5x-3y的最值．
  组卷：1900引用：4难度：0.3

  解析

• 24．如图，在直角坐标系中，点O是坐标原点，四边形OABC是平行四边形，点A的坐标为（14，0），点B的坐标为（18，

  4

  3

  ）．
  （1）求点C的坐标和平行四边形OABC的对称中心的点的坐标；
  （2）动点P从点O出发，沿OA方向以每秒1个单位的速度向终点A匀速运动，动点Q从点A出发，沿AB方向以每秒2个单位的速度向终点B匀速运动，一点到达终点时另一点停止运动．设点P运动的时间为t秒，求当t为何值时，△PQC的面积是平行四边形OABC的一半？
  （3）当△PQC的面积是平行四边形OABC面积的一半时，在平面直角坐标系中找到一点M，使以M、P、Q、C为顶点的四边形是平行四边形，请直接写出点M的坐标．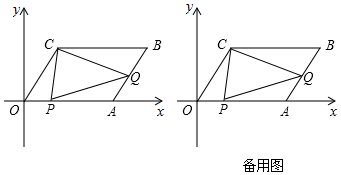
  
  组卷：1036引用：5难度：0.1

  解析