2022-2023学年江苏省泰州市姜堰实验中学七年级（上）独立作业数学试卷（二）

一、选择题（每题3分，共18分）

• 1．3的相反数是（　　）

  A．-3

  B．- 1 3

  C．3

  D． 1 3
  组卷：1561引用：535难度：0.9

  解析

• 2．下列各数是无理数的是（　　）

  A．-5	B． 22 7
  C．4.121121112	D． π 2
  组卷：195引用：4难度：0.9

  解析

• 3．下列各组中的两个单项式是同类项的是（　　）

  A．-3与a	B．2a2b与-3a2b
  C．3a3与2a2	D．a3b2与 1 2 a 2 b 3
  组卷：143引用：2难度：0.9

  解析

• 4．若x=2是关于x的方程2x+a=3的解，则a的值是（　　）

  A．1

  B．-1

  C．7

  D．-7
  组卷：925引用：17难度：0.9

  解析

• 5．如图，数轴上点A，M，B分别表示数a,a+b,b,那么下列运算结果一定是正数的是（　　）

  A．a+b

  B．a-b

  C．ab

  D．|a|-b
  组卷：2521引用：17难度：0.6

  解析

• 6．对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数，用min{a,b,c}表示这三个数中最小的数．例如：

  M

  {

  -

  1

  ，

  2

  ，

  3

  }

  =

  -

  1

  +

  2

  +

  3

  3

  =

  4

  3

  ，min{-1，2，3}=1，如果M{3，2x+1，x-1}=min{3，-x+7，2x+5}，那么x的值为（　　）

  A．2

  B．-3或0

  C．2或-4

  D．2或3
  组卷：94引用：2难度：0.5

  解析

二、填空题（每题3分，共30分）

• 7．-5πx²y³z的系数是

  ．
  组卷：56引用：3难度：0.8

  解析

• 8．比较大小：-7

  -8（用＞、＜或=号填空）．
  组卷：33引用：4难度：0.8

  解析

三、解答题（共102分）

• 25．我们规定：使得a-b=ab成立的一对数a,b为“积差等数对”，记为（a,b）．例如，因为1.5-0.6=1.5×0.6，（-2）-2=（-2）×2，所以数对（1.5，0.6），（-2，2）都是“积差等数对”．
  （1）下列数对中，是“积差等数对”的是

  ；
  ①（2，

  2

  3

  ）；②（1.5，3）；③（-

  1

  2

  ，-1）．
  （2）若（k,-3）是“积差等数对”，求k的值；
  （3）若（m,n）是“积差等数对”，求代数式4[3mn-m-2（mn-1）]-2（3m²-2n）+6m²的值．
  组卷：425引用：7难度：0.6

  解析

• 26．一科技小组进行机器人行走性能测试，已知MN是周长为360米的圆形跑道的直径，机器人A从M点出发，机器人B从N点出发，机器人A运动速度为每分钟a米，机器人B运动速度为每分钟b米，设行走的时间为t分钟．
  
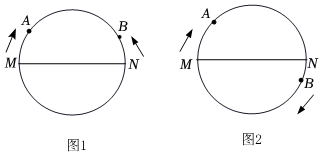
  （1）若a=15，b=5．
  ①若A顺时针转动，B逆时针转动，如图1，当t为多少分钟时，A与B第一次相遇；
  ②若同时顺时针运动，如图2，当机器人B第一次回到点N时，A与B相遇了

  次；
  （2）若a＞b,同时顺时针运动．
  ①当t=10分钟时，A与B第一次相遇．那么t为何值时，A、B两个机器人在圆形跑道上首次相距60米？
  ②若a=4b,试判断A与B第二次相遇位置，并说明理由．
  组卷：66引用：3难度：0.5

  解析