当前位置：试卷中心 > 试卷详情

2020年辽宁省大连市中考数学一模试卷

发布：2025/11/11 10:0:8

一、选择题（本题共10小题，每小题0分，共30分，在每小题给出的四个选项中，只有一个选项正确）

1．已知点A（a,2015）与点A′（-2016，b）是关于原点O的对称点，则a+b的值为（　　）
A．1 B．5 C．6 D．4
组卷：184引用：2难度：0.7
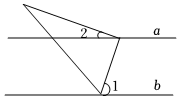2．如图，已知平行线a,b,一个直角三角板的直角顶点在直线a上，另一个顶点在直线b上，若∠1=70°，则∠2的大小为（　　）
A．15° B．20° C．25° D．30°
组卷：1682引用：16难度：0.7
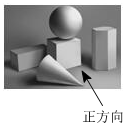3．佳佳练习几何体素描（如图），其中几何体的主视图是轴对称图形但不是中心对称图形的为（　　）
A．圆锥 B．正方体 C．圆柱 D．球
组卷：42引用：2难度：0.7
4．已知点（-1，y₁），（-2，y₂），（-4，y₃）在二次函数y=-2x²-8x+c的图象上，则y₁，y₂，y₃的大小关系是（　　）
A．y₁＜y₃＜y₂ B．y₃＜y₂＜y₁ C．y₃＜y₁＜y₂ D．y₂＜y₃＜y₁
组卷：144引用：3难度：0.6
5．一个长方形的三个顶点在平面直角坐标系中的坐标分别为（-1，-1），（-1，2），（3，-1），那么第四个顶点的坐标为（　　）
A．（3，2） B．（2，3） C．（3，3） D．（2，2）
组卷：296引用：2难度：0.5
6．某机械厂七月份生产零件50万个，九月份生产零件72万个．设该厂八九月份平均每月的增长率为x,那么x满足的方程是（　　）
A．500（1+x）²=72 B．50（1+x）=72
C．50（1+x）²=72 D．50（1+2x）=72
组卷：565引用：8难度：0.8
7．不论x,y为何有理数，x²+y²-10x+8y+45的值均为（　　）
A．正数 B．零 C．负数 D．非负数
组卷：1375引用：18难度：0.9
8．2020年11月24日22时06分，嫦娥五号探测器3000N发动机工作约2秒钟，顺利完成第一次轨道修正，继续飞向月球．截至第一次轨道修正前，嫦娥五号探测器各系统状态良好，已在轨飞行约17个小时，距离地球约16万千米，16万千米用科学记数法表示为（　　）
A．1.6×10⁴km B．1.6×10⁵km C．16×10⁴km D．0.16×10⁵km
组卷：65引用：3难度：0.8
9．在有理数2，-4，
1
3
，0中，最小的数是（　　）
A．2 B．-4 C．
1
3
D．0
组卷：24引用：2难度：0.9
10．某市初中学业水平实验操作考试要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试，小华和小强都抽到生物学科的概率是（　　）
A．
1
3
B．
1
4
C．
1
6
D．
1
9
组卷：302引用：13难度：0.6

二、填空题（本题共6小题，每小题3分，共18分）

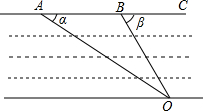11．如图，要测量一段两岸平行的河的宽度，在A点测得∠α=30°，在B点测得∠β=60°，且AB=50米，则这段河岸的宽度为
．
组卷：637引用：4难度：0.7
12．在一次捐款活动中，某班50名同学人人拿出自己的零花钱，有捐5元、10元、20元的，还有捐50元和100元的．如图统计图反映了不同捐款数的人数比例，那么该班同学平均每人捐款
元．
组卷：1730引用：43难度：0.5
13．不等式9x-2≤7x+3的解集是
．
组卷：28引用：1难度：0.7
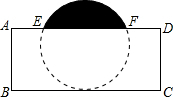14．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=
4
3
cm,CD=6cm,则该截面部分阴影的面积为
cm²．
组卷：68引用：1难度：0.5
15．如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数
y
=
k
x
（k≠0）的图象交于二、四象限的A、B两点，与x轴交于C点．已知A（-2，m），B（n,-2），tan∠BOC=
2
5
，则此一次函数的解析式为
．
组卷：1432引用：57难度：0.5
16．n支球队参加比赛，每两队之间进行一场比赛．写出比赛的场次数m与球队数n之间的关系式
．
组卷：415引用：3难度：0.6

三、解答题（本题共4小题，其中17、18、19题各9分，20题12分，共39分）

17．计算：
（1）（x+1）（x-4）+（x-2）²．
（2）（
2
x
x
-
1
-x）÷
x
2
-
9
x
-
1
．
组卷：20引用：1难度：0.7
18．在平面直角坐标系中，O为坐标原点，直线y=
4
3
x+4分别交y轴和x轴于点A、B两点，点C在x轴的正半轴上，AO=2OC，连接AC．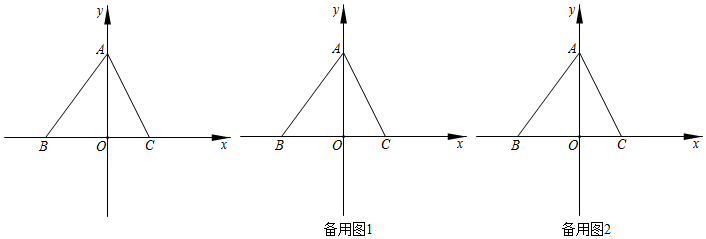

（1）如图1，求直线AC的解析式；
（2）如图2，点P在线段AB上，点Q在BC的延长线上，满足：AP=CQ，连接PQ交AC于点D，过点P作PE⊥AC于点E，设点P的横坐标为t,△PQE的面积为S，求S与t的函数关系式（不要求写出自变量t的取值范围）；
（3）如图3，在（2）的条件下，PQ交y轴于点M，过点A作AN⊥AC交QP的延长线于点N，过点Q作QF∥AC交PE的延长线于点F，若MN=DQ，求点F的坐标．
组卷：622引用：1难度：0.1
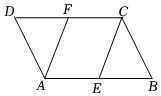19．如图，在▱ABCD中，E，F分别是AB，CD的中点，求证：AF=CE．
组卷：388引用：13难度：0.6
20．某地为了打造风光地带，将一段长为360米的河道整治任务由甲、乙两个工程队先后接力完成，共用20天，已知甲工程队每天整治20米，乙工程队每天整治16米，求甲、乙两个工程队分别整治了多长的河道．
组卷：681引用：1难度：0.5

四、解答题（本题共3小题，其中21题9分，22、23题各10分，共29分）

21．在△ABC中，AB=AC，∠BAC=90°．过点A作直线AP，点C关于直线AP的对称点为点D，连接BD，CD，直线BD交直线AP于点E．

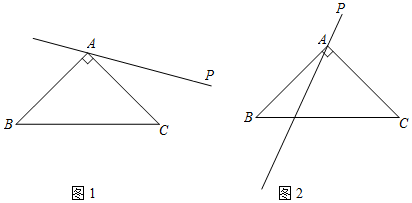
（1）依题意补全图1；
（2）在图1中，若∠PAC=30°，求∠ABD的度数；
（3）若直线AP旋转到如图2所示的位置，请用等式表示线段EB，ED，BC之间的数量关系，并证明．
组卷：632引用：2难度：0.2
22．甲、乙两人沿同一路线登山，图中线段OC、折线OAB分别是甲、乙两人登山的路程y（米）与登山时间x（分）之间的函数图象．请根据图象所提供的信息，解答如下问题：
（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量x的取值范围；
（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米？
组卷：3927引用：13难度：0.3
23．如图，在平面直角坐标系中，抛物线
y
=
-
1
2
x
2
-
x
+
c
与直线
l
1
：
y
=
-
2
3
x
+
4
相交于y轴上的点C，抛物线与x轴交于A，B两点（点A在点B的左侧）．
（1）求直线AC的解析式；
（2）如图1，连接BC，点P为直线AC、l₁之间第二象限抛物线上的一动点，过点P作PF∥y轴交直线l₁点F，过点P作PE∥BC交AC于点E，求
PF
+
8
5
5
PE
的最大值及此时点P的坐标；
（3）如图2，在（2）的条件下，将原抛物线沿射线PC方向平移
3
5
2
个单位长度，得到新抛物线y′，新抛物线y′与直线AC交于第一象限的点记为M，线段FC在直线l₁上运动，记运动中的点F为F′，点C为C′，当△F′C′M是以C′M为腰的等腰三角形时，请直接写出点C′的横坐标．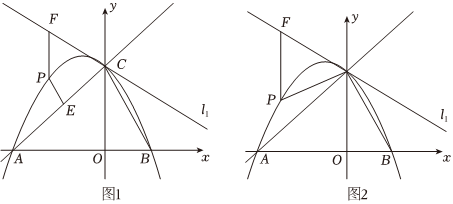
组卷：402引用：1难度：0.2

五、解答题（本题共3小题，其中24、25各题11分，26题12分，共34分）

24．体育委员统计了全班同学60秒跳绳的次数，并列出频数分布表．

次数 60≤x＜80 80≤x＜100 100≤x＜120 120≤x＜140 140≤x＜160 160≤x＜180

频数 2 4 21 13 8 4

（1）全班有多少学生？
（2）组距是多少？组数是多少？
（3）跳绳次数x在120≤x＜160范围的学生有多少？

组卷：821引用：6难度：0.1

25．计算：
42
÷
6
-
1
3
×
15
+|
7
-3|．
组卷：237引用：3难度：0.8
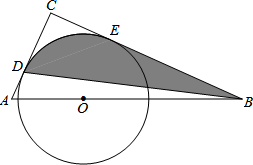26．如图，在△ABC中，∠C=90°，AC+BC=9，点O是斜边AB上一点，以O为圆心2为半径的圆分别与AC、BC相切于点D、E．
（1）求AC、BC的长；
（2）若AC=3，连接BD，求图中阴影部分的面积（π取3.14）．
组卷：355引用：60难度：0.5

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．500（1+x）²=72	B．50（1+x）=72
C．50（1+x）²=72	D．50（1+2x）=72

次数	60≤x＜80	80≤x＜100	100≤x＜120	120≤x＜140	140≤x＜160	160≤x＜180
频数	2	4	21	13	8	4

2020年辽宁省大连市中考数学一模试卷

一、选择题（本题共10小题，每小题0分，共30分，在每小题给出的四个选项中，只有一个选项正确）

1．已知点A（a,2015）与点A′（-2016，b）是关于原点O的对称点，则a+b的值为（ ）

2．如图，已知平行线a,b,一个直角三角板的直角顶点在直线a上，另一个顶点在直线b上，若∠1=70°，则∠2的大小为（ ）

3．佳佳练习几何体素描（如图），其中几何体的主视图是轴对称图形但不是中心对称图形的为（ ）

4．已知点（-1，y1），（-2，y2），（-4，y3）在二次函数y=-2x2-8x+c的图象上，则y1，y2，y3的大小关系是（ ）

5．一个长方形的三个顶点在平面直角坐标系中的坐标分别为（-1，-1），（-1，2），（3，-1），那么第四个顶点的坐标为（ ）

6．某机械厂七月份生产零件50万个，九月份生产零件72万个．设该厂八九月份平均每月的增长率为x,那么x满足的方程是（ ）

7．不论x,y为何有理数，x2+y2-10x+8y+45的值均为（ ）

9．在有理数2，-4，13，0中，最小的数是（ ）

10．某市初中学业水平实验操作考试要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试，小华和小强都抽到生物学科的概率是（ ）

二、填空题（本题共6小题，每小题3分，共18分）

11．如图，要测量一段两岸平行的河的宽度，在A点测得∠α=30°，在B点测得∠β=60°，且AB=50米，则这段河岸的宽度为．

12．在一次捐款活动中，某班50名同学人人拿出自己的零花钱，有捐5元、10元、20元的，还有捐50元和100元的．如图统计图反映了不同捐款数的人数比例，那么该班同学平均每人捐款元．

13．不等式9x-2≤7x+3的解集是 ．

14．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=43cm,CD=6cm,则该截面部分阴影的面积为cm2．

15．如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=kx（k≠0）的图象交于二、四象限的A、B两点，与x轴交于C点．已知A（-2，m），B（n,-2），tan∠BOC=25，则此一次函数的解析式为．

16．n支球队参加比赛，每两队之间进行一场比赛．写出比赛的场次数m与球队数n之间的关系式．

三、解答题（本题共4小题，其中17、18、19题各9分，20题12分，共39分）

17．计算：（1）（x+1）（x-4）+（x-2）2．（2）（2xx-1-x）÷x2-9x-1．

19．如图，在▱ABCD中，E，F分别是AB，CD的中点，求证：AF=CE．

20．某地为了打造风光地带，将一段长为360米的河道整治任务由甲、乙两个工程队先后接力完成，共用20天，已知甲工程队每天整治20米，乙工程队每天整治16米，求甲、乙两个工程队分别整治了多长的河道．

四、解答题（本题共3小题，其中21题9分，22、23题各10分，共29分）

五、解答题（本题共3小题，其中24、25各题11分，26题12分，共34分）

25．计算：42÷6-13×15+|7-3|．

26．如图，在△ABC中，∠C=90°，AC+BC=9，点O是斜边AB上一点，以O为圆心2为半径的圆分别与AC、BC相切于点D、E．（1）求AC、BC的长；（2）若AC=3，连接BD，求图中阴影部分的面积（π取3.14）．

1．已知点A（a,2015）与点A′（-2016，b）是关于原点O的对称点，则a+b的值为（　　）

2．如图，已知平行线a,b,一个直角三角板的直角顶点在直线a上，另一个顶点在直线b上，若∠1=70°，则∠2的大小为（　　）

3．佳佳练习几何体素描（如图），其中几何体的主视图是轴对称图形但不是中心对称图形的为（　　）

4．已知点（-1，y₁），（-2，y₂），（-4，y₃）在二次函数y=-2x²-8x+c的图象上，则y₁，y₂，y₃的大小关系是（　　）

5．一个长方形的三个顶点在平面直角坐标系中的坐标分别为（-1，-1），（-1，2），（3，-1），那么第四个顶点的坐标为（　　）

6．某机械厂七月份生产零件50万个，九月份生产零件72万个．设该厂八九月份平均每月的增长率为x,那么x满足的方程是（　　）

7．不论x,y为何有理数，x²+y²-10x+8y+45的值均为（　　）

9．在有理数2，-4，
1
3
，0中，最小的数是（　　）

10．某市初中学业水平实验操作考试要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试，小华和小强都抽到生物学科的概率是（　　）

11．如图，要测量一段两岸平行的河的宽度，在A点测得∠α=30°，在B点测得∠β=60°，且AB=50米，则这段河岸的宽度为
．

12．在一次捐款活动中，某班50名同学人人拿出自己的零花钱，有捐5元、10元、20元的，还有捐50元和100元的．如图统计图反映了不同捐款数的人数比例，那么该班同学平均每人捐款
元．

13．不等式9x-2≤7x+3的解集是
．

14．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=
4
3
cm,CD=6cm,则该截面部分阴影的面积为
cm²．

15．如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数
y
=
k
x
（k≠0）的图象交于二、四象限的A、B两点，与x轴交于C点．已知A（-2，m），B（n,-2），tan∠BOC=
2
5
，则此一次函数的解析式为
．

16．n支球队参加比赛，每两队之间进行一场比赛．写出比赛的场次数m与球队数n之间的关系式
．

17．计算：
（1）（x+1）（x-4）+（x-2）²．
（2）（
2
x
x
-
1
-x）÷
x
2
-
9
x
-
1
．

25．计算：
42
÷
6
-
1
3
×
15
+|
7
-3|．

26．如图，在△ABC中，∠C=90°，AC+BC=9，点O是斜边AB上一点，以O为圆心2为半径的圆分别与AC、BC相切于点D、E．
（1）求AC、BC的长；
（2）若AC=3，连接BD，求图中阴影部分的面积（π取3.14）．