2019-2020学年湖北省随州市曾都区九年级（上）期末数学试卷

一、选择题：本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

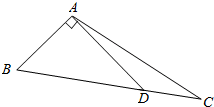• 1．如图，在直角△BAD中，延长斜边BD到点C，使DC=

  1

  2

  BD，连接AC，若tanB=

  5

  3

  ，则tan∠CAD的值（　　）

  A． 3 3

  B． 3 5

  C． 1 3

  D． 1 5
  组卷：2893引用：71难度：0.5

  解析

• 2．如图，AB是⊙O的直径，点C、D在⊙O上，且点C、D在AB的异侧，连接AD、BD、OD、OC，若∠ABD=15°，且AD∥OC，则∠BOC的度数为（　　）

  A．120°

  B．105°

  C．100°

  D．110°
  组卷：817引用：5难度：0.6

  解析

• 3．甲、乙两地相距60km,则汽车由甲地行驶到乙地所用时间y（小时）与行驶速度x（千米/时）之间的函数图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：429引用：37难度：0.9

  解析

• 4．如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．连接AC，若AH平分∠CAD，且正方形EFGH的面积为3，则正方形ABCD的面积为（　　）

  A． 6 + 3 2

  B． 4 + 2 2

  C． 6 + 2 3

  D．15
  组卷：2010引用：6难度：0.3

  解析

• 5．把一元二次方程x²+2x=5（x-2）化成一般形式，则a,b,c的值分别是（　　）

  A．1，-3，2

  B．1，7，-10

  C．1，-5，12

  D．1，-3，10
  组卷：716引用：4难度：0.8

  解析

• 6．在线段、角、等边三角形、等腰三角形、等腰梯形、平行四边形、矩形和圆这几种图形中，既是轴对称图形又是中心对称图形的图形有（　　）个．

  A．2

  B．3

  C．4

  D．5
  组卷：42引用：1难度：0.9

  解析

• 7．一个扇形的半径为8cm,弧长为

  16

  3

  π

  cm,则扇形的圆心角为（　　）

  A．60°

  B．120°

  C．150°

  D．180°
  组卷：1532引用：56难度：0.9

  解析

• 8．如图，二次函数y=ax²+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x₁，x₂，其中-1＜x₁＜0，1＜x₂＜2，下列结论：①4a+2b+c＜0，②2a+b＜0，③b²+8a＞4ac,④a＜-1，其中结论正确的有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：9215引用：25难度：0.7

  解析

• 9．袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（　　）

  A．摸出的三个球中至少有两个球是黑球

  B．摸出的三个球中至少有两个球是白球

  C．摸出的三个球中至少有一个球是黑球

  D．摸出的三个球中至少有一个球是白球
  组卷：356引用：6难度：0.9

  解析

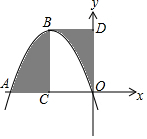• 10．如图，在平面直角坐标系中，抛物线y=-

  2

  3

  （x+3）²+k经过坐标原点O，与x轴的另一个交点为A．过抛物线的顶点B分别作BC⊥x轴于点C、BD⊥y轴于点D，则图中阴影部分图形的面积和为（　　）

  A．18

  B．12

  C．9

  D．6
  组卷：685引用：3难度：0.4

  解析

二、填空题（本题共6小题，每小题3分，共18分，将答案填在答题纸上）

• 11．如图，在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A₁B₁C₁．点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P₁，线段EP₁长度的最小值是

  ．
  组卷：1184引用：9难度：0.7

  解析

• 12．如图在平面直角坐标系中，矩形OABC的顶点坐标分别是O（0，0），C（6，0），B（6，4），A（0，4），已知矩形OA'B'C与矩形OABC位似，位似中心是原点O，矩形OA'BC'的面积等于矩形OABC面积的

  1

  4

  ，且点B不在第一象限，则点B的坐标是

  ．
  组卷：21引用：1难度：0.7

  解析

• 13．某中学组织初二学生开展篮球比赛，以班为单位单循环形式（每两班之间赛一场），现计划安排15场比赛，则共有多少个班级参赛？设有x个班级参赛，根据题意，可列方程为

  ．
  组卷：548引用：5难度：0.6

  解析

• 14．三角形的三条中线相交于一点，这个点一定在三角形的内部，这个点叫做三角形的

  ．
  组卷：112引用：1难度：0.9

  解析

• 15．反比例函数y=

  k

  x

  （k≠0）的图象经过P，如图所示，根据图象可知，反比例函数的解析式为

   

  ．
  组卷：62引用：22难度：0.9

  解析

• 16．把二次函数y=x²-12x化为形如y=a（x-h）²+k的形式

  ．
  组卷：4797引用：73难度：0.7

  解析

三、解答题：本题共8小题，共72分.解答应写出文字说明、证明过程或演算步骤.

• 17．探究与证明．
  已知四边形ABCD中，M，N分别是AB，AD边上的点，DM与CN交于点Q．
  【初探】（1）①如图1，若四边形ABCD是正方形，且DM⊥CN于点Q，则

  DM

  CN

  =

  ；
  ②如图2，若四边形ABCD是矩形，且DM⊥CN，求证：

  DM

  CN

  =

  AD

  CD

  ；
  【延伸】（2）如图3，若四边形ABCD是平行四边形，且∠B+∠MQC=180°，求证：

  DM

  CN

  =

  AD

  CD

  ；
  【拓展】如图4，若BA=BC=5，DA=DC=10，∠BAD=90°，DM⊥CN，请直接写出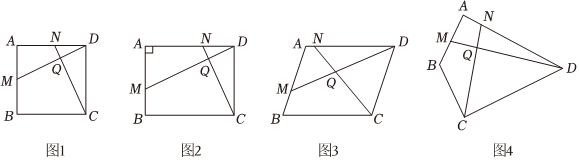

  DM

  CN

  的值．
  ​
  组卷：155引用：2难度：0.3

  解析

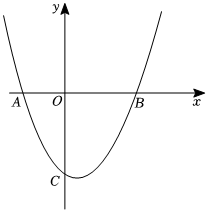• 18．如图，二次函数y=ax²+bx+c的图象交x轴于A（-1，0），B（2，0），交y轴于C（0，-2）．
  （1）求二次函数的解析式；
  （2）点P在该二次函数图象的对称轴上，且使|PB-PC|最大，求点P的坐标；
  （3）若点M为该二次函数图象在第四象限内一个动点，当点M运动到何处时，四边形ACMB的面积最大？求出此时点M的坐标及四边形ACMB面积的最大值．
  组卷：564引用：1难度：0.3

  解析

• 19．国家教育部规定：初中生睡眠时间应达到9个小时，某中学对全体初中生就睡眠的时长进行抽样调查，调查结果共分为四个层次：A．8小时以下；B．8～9小时；C．9～10小时；D．10小时以上．根据调查统计结果绘制以下两幅不完整的统计图．请结合统计图，回答下列问题：
  （1）本次参与调查的学生共有多少人？并补全条形统计图；
  （2）求扇形统计图中层次B的圆心角度数；
  （3）睡眠时间8小时以下的3名同学中有一名男生和二名女生，若心理老师想从这3名同学中任选两名同学进行交流，请用画树状图或列表的方法求同时选出的两名同学是一名男生和一名女生的概率．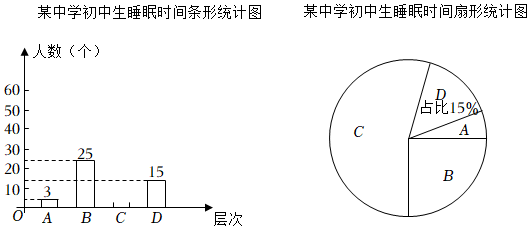
  
  组卷：71引用：5难度：0.5

  解析

• 20．已知关于x的方程x²+2mx+m²-1=0．
  （1）求证：此方程有两个不相等的实数根；
  （2）设此方程的两个根分别为x₁，x₂，若x₁+x₂=6，请解此方程．
  组卷：121引用：5难度：0.6

  解析

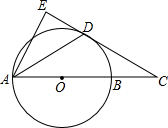• 21．如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D，且AE⊥CD，垂足为点E．
  （1）求证：直线CE是⊙O的切线；
  （2）若BC=6，CD=6

  2

  ，求弦AD的长．
  组卷：618引用：2难度：0.5

  解析

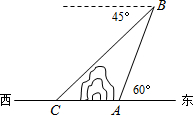• 22．小王是一名经验丰富的户外搜救人员，某日小王接到搜救任务去山里救助一名受伤的户外运动员；来到这座山的东侧A处，为了方便确定受伤人员具体位置，他在A处向上放出一架无人机搜寻，该无人机以每分钟60m的速度沿着仰角为60°的方向上升，5分钟后升到B处，这时小王通过无人机发现受伤人员在他的正西方向，且从无人机上看，受伤人员在它的俯角为45°方向，求小王与受伤人员间AC的距离．（结果保留根号）
  组卷：386引用：4难度：0.5

  解析

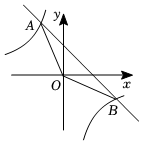• 23．如图，直线y=-x+2与反比例函数

  y

  =

  k

  x

  的图象相交于A（a,3），B两点．
  （1）求该反比例函数的表达式；
  （2）求△AOB的面积．
  组卷：108引用：1难度：0.6

  解析

• 24．如图，有长为24m的篱笆，一面利用墙（墙的最大可用长度a为10m）围成中间隔有一道篱笆的矩形花圃，设花圃的宽AB为x m,面积为Sm²．
  （1）求S与x的函数表达式．
  （2）如果要围成面积为45m²的花圃，AB的长是多少米？
  （3）能围成面积为50m²的花圃吗？若能，请说明围法；若不能请说明理由．
  组卷：1175引用：3难度：0.5

  解析