2022-2023学年山东省济宁市曲阜市八年级（上）期中数学试卷

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项符合题目要求.

• 1．下列疫情防控宣传图片中，是轴对称图形的是（　　）

  A． 勤洗手，勤通风	B． 打喷嚏，捂口鼻
  C． 有症状，早就医	D． 防控疫情，我们在一起
  组卷：197引用：17难度：0.9

  解析

• 2．用下列长度的三根木棒首尾相接，能做成三角形框架的是（　　）

  A．2cm、3cm、4cm	B．2cm、2cm、5cm
  C．1cm、5cm、3cm	D．2cm、5cm、8cm
  组卷：6引用：1难度：0.6

  解析

• 3．人字梯中间一般会设计一“拉杆”，这样做的道理是（　　）

  A．两点之间，线段最短

  B．垂线段最短

  C．两直线平行，内错角相等

  D．三角形具有稳定性
  组卷：4399引用：72难度：0.8

  解析

• 4．在平面直角坐标系中，已知点A（2，m）和点B（n,-3）关于x轴对称，则m+n的值是（　　）

  A．-1

  B．1

  C．5

  D．-5
  组卷：2222引用：34难度：0.7

  解析

• 5．如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（　　）

  A．∠A=∠D

  B．AB=DC

  C．∠ACB=∠DBC

  D．AC=BD
  组卷：6366引用：147难度：0.9

  解析

• 6．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（　　）

  A．40°

  B．45°

  C．50°

  D．55°
  组卷：4712引用：61难度：0.9

  解析

• 7．如图所示，将正方形纸片三次对折后，沿图中AB线剪掉一个等腰直角三角形，展开铺平得到的图形是（　　）
  

  A．

  B．

  C．

  D．
  组卷：1491引用：57难度：0.9

  解析

三、解答题（共7小题，共55分）

• 21．如果一个三角形能被一条线段割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．
  
  （1）如图1，△ABC是等腰锐角三角形，AB=AC（AB＞BC），若∠ABC的角平分线BD交AC于点D，且BD是△ABC的一条特异线，则∠BDC=

  度．
  （2）如图2，△ABC中，∠B=2∠C，线段AC的垂直平分线交AC于点D，交BC于点E．
  求证：AE是△ABC的一条特异线；
  （3）如图3，若△ABC是特异三角形，∠A=30°，∠B为钝角，不写过程，直接写出所有可能的∠C的度数．
  组卷：143引用：2难度：0.4

  解析

• 22．（1）如图1，在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m,CE⊥直线m,垂足分别为D，E．求证：DE=BD+CE；
  
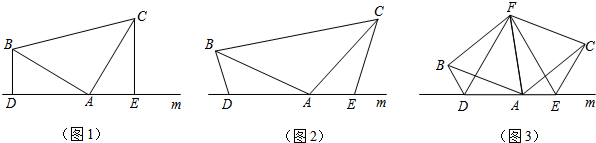
  （2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D，A，E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角，请问结论DE=BD+CE是否成立？若成立，请你给出证明；若不成立，请说明理由；
  （3）如图3，在（2）的条件下，若a=120°，且△ACF为等边三角形，试判断△DEF的形状，并说明理由．
  组卷：2820引用：12难度：0.2

  解析