2022-2023学年广东省汕头市澄海区八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．下列各式中是最简二次根式的是（　　）

  A． 15

  B． 20

  C． 27

  D． 1 5
  组卷：18引用：1难度：0.7

  解析

• 2．一个底面是长方形的小塑料盒，长为40cm,宽为30cm,在小塑料盒底面放一根木棒，那么这根木棒最长（不计木棒粗细）可以是（　　）

  A．30cm

  B．40cm

  C．50cm

  D． 10 7 cm
  组卷：88引用：1难度：0.8

  解析

• 3．一次函数y=-2x+1的图象不经过（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：2731引用：97难度：0.9

  解析

• 4．在一次歌咏比赛中，某选手的得分情况如下：92，88，95，93，96，95，94．这组数据的众数和中位数分别是（　　）

  A．94，94

  B．95，95

  C．94，95

  D．95，94
  组卷：167引用：63难度：0.9

  解析

• 5．已知关于x的一次函数y=（2k-1）x+1，y值随x的增大而减小，则k的值可以是（　　）

  A．2

  B．1

  C． 2 3

  D．-1
  组卷：79引用：1难度：0.5

  解析

• 6．若式子

  x

  +

  2

  x

  -

  1

  有意义，则x的取值范围是（　　）

  A．x≥-2

  B．x＞1

  C．x＞-2且x≠1

  D．x≥-2且x≠1
  组卷：197引用：17难度：0.9

  解析

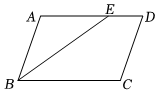• 7．如图，在▱ABCD中，∠ABC的平分线BE交AD于点E，若∠CBE=32°，则∠C的度数为（　　）

  A．112°

  B．116°

  C．128°

  D．148°
  组卷：26引用：1难度：0.6

  解析

五、解答题（三）（本大题共2小题，每小题12分，共24分）

• 22．如图，在▱ABCD中，AD=2CD，F是AD的中点，CE⊥AB，垂足为点E，连接EF、CF．
  （1）求证：CF平分∠BCD；
  （2）若BE=5，CE=12，求△ECF的面积；
  （3）请判断线段EF与CF的数量关系，并说明理由．
  组卷：55引用：2难度：0.3

  解析

• 23．如图，在平面直角坐标系中，直线l₁：y=-x+5与y轴交于点A，直线l₂：y=kx+b与x轴、y轴分别交于点B（-4，0）和点C，直线l₁与直线l₂交于点D（2，a）．
  （1）求直线l₂的解析式；
  （2）若点E为直线l₂上一个动点，过点E作EF⊥x轴，垂足为F，且与直线l₁交于点G．设F（m,0），求△DEG的面积（用含m的式子表示）；
  （3）问在平面内是否存在点M，使得以点A、C、D、M为顶点的四边形是平行四边形，若存在，求出点M的坐标；若不存在，请说明理由．
  
  组卷：189引用：4难度：0.3

  解析