2023-2024学年广东省惠州一中八年级(上)期中数学试卷
发布:2024/10/4 6:0:3
一、单选题:本大题共10小题,每小题3分,共30分.
-
1.下列冰雪运动项目的图标中,是轴对称图形的是( )
组卷:648引用:13难度:0.9 -
2.若一个三角形的两边长分别为4cm,6cm,则它的第三边的长可以是( )
组卷:50引用:3难度:0.7 -
3.下列四个图形中,线段BE是△ABC的高的是( )
组卷:269引用:25难度:0.7 -
4.点A(3,-1)关于x轴的对称点是( )
组卷:112引用:10难度:0.7 -
5.已知一个正多边形的每个外角都等于72°,则这个正多边形是( )
组卷:750引用:14难度:0.7 -
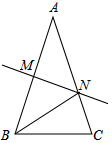 6.如图,在△ABC中,AB=AC,MN是AB的垂直平分线,△BNC的周长是24cm,BC=10cm,则AB的长是( )组卷:614引用:7难度:0.7
6.如图,在△ABC中,AB=AC,MN是AB的垂直平分线,△BNC的周长是24cm,BC=10cm,则AB的长是( )组卷:614引用:7难度:0.7 -
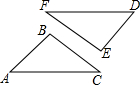 7.如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )组卷:513引用:10难度:0.9
7.如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )组卷:513引用:10难度:0.9
五、解答题(三):本大题共2小题,每小题12分,共24分.
-
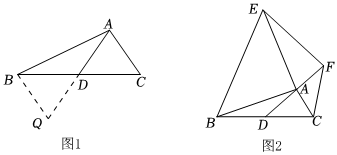 22.阅读理解:课外兴趣小组活动时,老师提出了如下问题:在△ABC中,AB=7,AC=3,求BC边上的中线AD的取值范围.
22.阅读理解:课外兴趣小组活动时,老师提出了如下问题:在△ABC中,AB=7,AC=3,求BC边上的中线AD的取值范围.
(1)小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;③利用三角形的三边关系可得4<AQ<10,则AD的取值范围是 .
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)请写出图1中AC与BQ的位置关系并证明;
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°,试探究线段AD与EF的数量和位置关系,并加以证明.组卷:908引用:17难度:0.4 -
23.如图1,E点在BC上,∠A=∠D,∠ACB+∠BED=180°.
(1)求证:AB∥CD;
(2)如图2,AB∥CD,BG平分∠ABE,与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数;
(3)如图3,若∠DEB=α,AB∥CD,BM平分∠EBK,DN平分∠CDE,作BP∥DN,直接写出∠PBM与α的关系.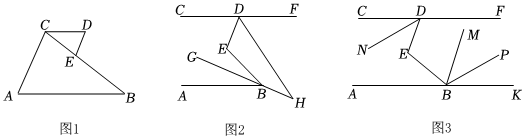 组卷:168引用:2难度:0.2
组卷:168引用:2难度:0.2


