当前位置：试卷中心 > 试卷详情

2023年山西省大同市新荣区两校联考中考数学三模试卷

发布：2024/7/3 8:0:9

一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求）

1．若数轴上点A，B分别表示数3，-2，则A，B两点之间的距离可表示为（　　）
A．3-（-2） B．3+（-2） C．（-2）+3 D．（-2）-3
组卷：644引用：3难度：0.8
解析
2．“鼠牛虎兔龙蛇马，羊猴鸡狗猪娃娃”，十二生肖是中华儿女独特的生命密码和文化符号．下列图案是生肖艺术展的部分剪纸图案，其中图案是轴对称图形的是（　　）
A． B． C． D．
组卷：19引用：1难度：0.9
解析
3．某校为提升教职工的身体素质，开展了“放飞心情、健行健康”为主体的健步走活动，李老师用计步器记录自己一个月（30天）每天走的步数，并绘制成如下统计表：

步数（万步） 1.1 1.2 1.3 1.4 1.5

天数 2 3 10 12 3

在每天所走的步数这组数据中、众数和中位数分别是（　　）
A．1.4，1.35 B．1.4，1.4 C．1.5，1.3 D．1.4，1.2
组卷：24引用：1难度：0.7
解析
4．原子是化学变化中的最小微粒，按照国际单位制的规定，质量单位是“千克”．例如：1个氧原子的质量是2.657×10^-26kg.如果小数0.000…02657用科学记数法表示为2.657×10^-26，则这个小数中“0”的个数是（　　）
A．25个 B．26个 C．27个 D．28个
组卷：160引用：5难度：0.8
解析
5．计算
a
2
-
1
a
2
-
2
a
+
1
•
1
-
a
a
2
+
a
的结果为（　　）
A．
-
1
a
B．
1
a
C．
2
a
D．
3
a
组卷：533引用：1难度：0.7
解析
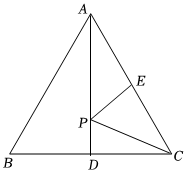6．如图，△ABC是等边三角形，AD是BC边上的高，点E是AC边的中点，点P是AD上的一个动点，当PC+PE最小时，∠PCD的度数是（　　）
A．90° B．60° C．45° D．30°
组卷：308引用：1难度：0.5
解析
7．中国清代算书《御制数理精蕴》（卷九）中有这样一题：“设如有铜铸甲、乙两钟，未称斤数，但云取乙钟铜八十斤入甲钟，则所余得甲钟四分之一；取甲钟铜八十斤入乙钟，则所余得乙钟三分之二；问二钟各得铜数若干？”设甲钟为x斤，乙钟为y斤，根据题意可列方程组为（　　）
A．
1
4
（
x
-
80
）
=
y
+
80
，
x
-
80
=
2
3
（
y
+
80
）
B．
1
4
（
x
-
80
）
=
y
-
80
，
x
+
80
=
2
3
（
y
-
80
）
C．
1
4
（
x
-
80
）
=
y
+
80
，
x
+
80
=
2
3
（
y
-
80
）
D．
1
4
（
x
+
80
）
=
y
-
80
，
x
-
80
=
2
3
（
y
+
80
）
组卷：83引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8个小题，共75分．解答应写出文字说明、证明过程或演算步骤）

22．综合与实践：
问题情景：如图1、正方形ABCD与正方形AEFG的边AB，AE（AB＜AE）在一条直线上，正方形AEFG以点A为旋转中心逆时针旋转，设旋转角为α，在旋转过程中，两个正方形只有点A重合，其它顶点均不重合，连接BE，DG．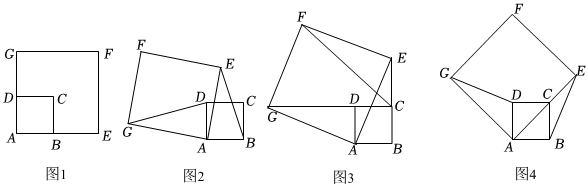

操作发现：（1）当正方形AEFG旋转至如图2所示的位置时，求证：BE=DG；
（2）如图3，当点E在BC延长线上时，连接FC，求∠FCE的度数；
问题解决：（3）如图4，如果α=45°，AB=2，AE=4
2
，请直接写出点G到BE的距离．
组卷：230引用：2难度：0.5
解析
23．综合与探究：
如图，抛物线
y
=
3
4
x
2
-
3
2
x
-
6
与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点D是抛物线上一个动点，设点D的横坐标为m（1＜m＜4），连接AC，BC，DC，DB．

（1）求A，B，C三点的坐标；
（2）当△BCD的面积等于△AOC的面积的
3
4
时，求m的值；
（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试探究是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，请直接写出点M的坐标；若不存在，请说明理由．
组卷：184引用：1难度：0.1
解析