2022-2023学年广东省惠州市惠阳区东升学校八年级（上）月考数学试卷（9月份）

一、选择题（共10小题，每小题3分，满分30分）

• 1．下列各组数中，不能成为三角形三条边长的数是（　　）

  A．5，10，12

  B．3，14，13

  C．4，12，12

  D．2，6，8
  组卷：300引用：5难度：0.8

  解析

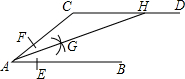• 2．如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB、AC于E、F两点；再分别以E、F为圆心，大于

  1

  2

  EF长为半径作圆弧，两条圆弧交于点G，作射线AG交CD于点H．若∠C=140°，则∠AHC的大小是（　　）

  A．20°

  B．25°

  C．30°

  D．40°
  组卷：1076引用：7难度：0.7

  解析

• 3．三角形的一个内角等于其余两个内角的和，则这个三角形必定是（　　）

  A．锐角三角形

  B．直角三角形

  C．钝角三角形

  D．等腰三角形
  组卷：30引用：4难度：0.8

  解析

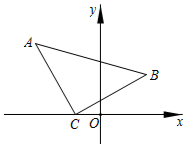• 4．如图，将一块含45°角的直角三角板ABC放置在直角坐标系中，直角顶点C（-1，0），点B（a,b）在第一象限，则点A的坐标为（　　）

  A．（a-1，b+1）

  B．（-b-1，a+1）

  C．（b+1，a+1）

  D．（-b-1，a-1）
  组卷：395引用：2难度：0.6

  解析

• 5．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④AD平分∠CDE；其中正确的个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：372引用：6难度：0.6

  解析

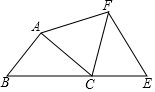• 6．如图，点B，C，E在同一条直线上，∠B=∠E=∠ACF=60°，AB=CE，则与线段BC相等的线段是（　　）

  A．AC

  B．AF

  C．CF

  D．EF
  组卷：1262引用：5难度：0.5

  解析

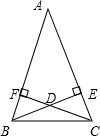• 7．如图，AB=AC，BE⊥AC于E，CF⊥AB于F，BE，CF交于D，则以下结论：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．正确的是（　　）

  A．①

  B．②

  C．①②

  D．①②③
  组卷：2741引用：23难度：0.7

  解析

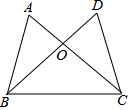• 8．如图，已知AC=BD，OA=OD，给出下列四个结论：①∠ACB=∠CBD；②△AOB≌△COD；③AB=CD；④△BOC是直角三角形，其中正确的有（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：369引用：4难度：0.5

  解析

三、解答题（共8题，共62分）

• 24．在△ABC中，AB=AC，点D是直线BC上一动点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，BC=4，连接CE．
  
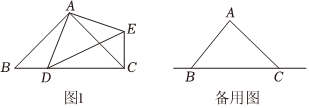
  （1）如图1，点D在边BC上，求证：△ABD≌△ACE．
  （2）在（1）的条件下，若∠BAC=90°，求证：EC⊥BC．
  （3）若∠BAC=90°，DC=1，则S_△DCE=

  ．
  组卷：34引用：2难度：0.5

  解析

• 25．（1）在锐角△ABC中，BC边上的高所在直线和AB边上的高所在直线的交点为P，∠APC=110°，求∠B的度数；
  （2）如图1，AF和CE分别平分∠BAD和∠BCD．当点D在直线AC上时，∠APC=100°，则∠B的度数；
  （3）在（2）的基础上，当点D在直线AC外时，如图2：∠ADC=130°，∠APC=100°，求∠B的度数．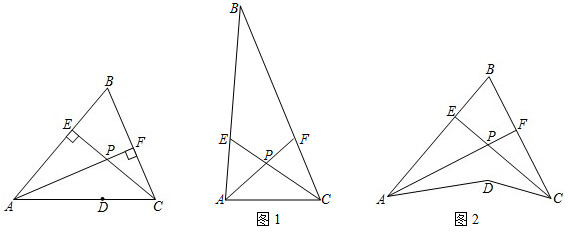
  
  组卷：1021引用：3难度：0.5

  解析