2021-2022学年河南省许昌市建安区九年级（上）期中数学试卷

一、选择题（每小题3分，共30分）

• 1．在10×10的正方形网格纸上，每个小正方形的边长都为1．如果以该网格中心为圆心，以5为半径画圆，那么在该圆周上的格点共有（　　）

  A．4个

  B．8个

  C．12个

  D．16个
  组卷：63引用：1难度：0.9

  解析

• 2．解下面方程：（1）（x-2）²=5，（2）x²-3x-2=0，（3）x²+x-6=0，较适当的方法分别为（　　）

  A．（1）直接开平方法（2）因式分解法（3）配方法

  B．（1）因式分解法（2）公式法（3）直接开平方法

  C．（1）公式法（2）直接开平方法（3）因式分解法

  D．（1）直接开平方法（2）公式法（3）因式分解法
  组卷：193引用：17难度：0.9

  解析

• 3．下列图形中，既是轴对称又是中心对称的图形是（　　）

  A．平行四边形

  B．等腰梯形

  C．等边三角形

  D．圆
  组卷：7引用：1难度：0.9

  解析

• 4．有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（　　）

  A． 1 2  x（x-1）=45	B． 1 2  x（x+1）=45
  C．x（x-1）=45	D．x（x+1）=45
  组卷：2078引用：74难度：0.7

  解析

• 5．关于x的方程x²+2kx-k-1=0的根的情况描述正确的是（　　）

  A．k为任何实数，方程都没有实数根

  B．k为任何实数，方程都有两个不相等的实数根

  C．k为任何实数，方程都有两个相等的实数根

  D．根据k的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种
  组卷：42引用：3难度：0.9

  解析

• 6．将抛物线y=-（x+1）²+4的图象向右平移1个单位，再向下平移2个单位，得到的抛物线必定经过点（　　）

  A．（-2，2）

  B．（-1，1）

  C．（0，6）

  D．（1，-3）
  组卷：310引用：6难度：0.6

  解析

• 7．若函数y=mx²+（m+2）x+

  1

  2

  m+1的图象与x轴只有一个交点，那么m的值为（　　）

  A．0

  B．0或2

  C．2或-2

  D．0，2或-2
  组卷：7346引用：86难度：0.5

  解析

• 8．下列语句中，正确的是（　　）

  A．在同圆或等圆中，相等的圆心角所对的弧相等

  B．三点确定一个圆

  C．三角形的外心到三角形的三边距离相等

  D．长度相等的两条弧是等弧
  组卷：197引用：1难度：0.7

  解析

• 9．函数y=ax²与函数y=ax+a（a≠0），在同一平面直角坐标系中的图象大致是图中的（　　）

  A．

  B．

  C．

  D．
  组卷：1499引用：3难度：0.6

  解析

• 10．如图，在△AOB中，已知∠AOB=90°，AO=3，BO=4．将△AOB绕顶点O按顺时针方向旋转α（0°＜α＜90°）到△A₁OB₁处，此时线段OB₁与边AB的交点为点D，则在旋转过程中，线段B₁D长的最大值为（　　）

  A．4.5

  B．5

  C． 12 5

  D． 8 5
  组卷：952引用：6难度：0.6

  解析

二、填空题（每小题3分，共15分）

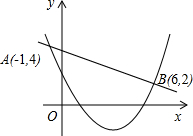• 11．已知二次函数y₁=ax²+bx+c（a≠0）与一次函数y₂=kx+m（k≠0）的图象交于点A（-1，4），B（6，2）（如图所示），则能使y₁＞y₂成立的x的取值范围是

   

  ．
  组卷：223引用：3难度：0.7

  解析

• 12．一元二次方程x²-9x=0的根是

  ．
  组卷：171引用：4难度：0.7

  解析

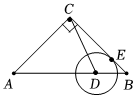• 13．如图，△ABC中，AC=BC=4，∠ACB=90°，D为边AB上一动点（不与A、B重合），⊙D与BC切于E点，E点关于CD的对称点F在△ABC的一边上，则BD=

  ．
  组卷：15引用：1难度：0.6

  解析

• 14．若x=2是关于x的一元二次方程x²-2kx+3k-2=0的解，则k=

  ．
  组卷：152引用：3难度：0.5

  解析

• 15．点A与点P（-2，1）关于y轴对称，点B与点A关于原点对称，则点B的点坐标为

   

  ．
  组卷：30引用：1难度：0.7

  解析

三、解答题（共75分）

• 16．为满足市场需求，某超市在春节来临前夕，购进一种品牌汤圆，每盒进价是20元，超市规定每盒售价不得少于25元．根据以往销售经验发现：当售价定为每盒25元时，每天可卖出350盒，每盒售价每提高1元，每天要少卖出10盒．
  （1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；
  （2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
  （3）为稳定物价，有关管理部门限定：这种汤圆的每盒售价不得高于35元．如果超市想要每天获得不低于3000元的利润，那么超市每天至少销售汤圆多少盒？
  组卷：293引用：1难度：0.3

  解析

• 17．已知二次函数y=ax²+bx+c图象的对称轴是直线x=1，且图象过点A（3，0）和点B（-2，5），求此函数的解析式．
  组卷：99引用：3难度：0.5

  解析

• 18．如图是从独轮车中抽象出来的几何模型，在△ABC中，AC=AB，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E，连接OE．
  （1）求证：DE是⊙O的切线；
  （2）若BC=12，∠ACB=30°，求线段OE的长．
  组卷：133引用：1难度：0.6

  解析

• 19．湖水清清味道甜，湖中草嫩螃蟹鲜．某种规格的溱湖簖蟹养殖成本为30元/只，根据市场调查发现，售价为50元/只时，每天可销售400只，为增大市场占有率，在保证盈利的情况下，养殖户采取降价措施，一只蟹的售价每降低1元，每天销量可增加40只．
  （1）当降价2元/只时，养殖户每天可售　

  　只螃蟹；
  （2）若养殖户每天的利润要达到8840元，并尽可能让利顾客，则售价应为多少元；
  （3）当每只售价多少元时，每天销售的利润y（元）最大，最大利润是多少．
  组卷：13引用：2难度：0.5

  解析

• 20．已知关于x的一元二次方程mx²-4x+1=0．
  （1）若1是该方程mx²-4x+1=0的一个根，求m的值；
  （2）若一元二次方程mx²-4x+1=0有实数根，求m的取值范围．
  组卷：917引用：4难度：0.5

  解析

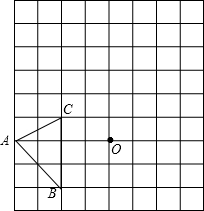• 21．如图，在边长均为1的正方形网格纸上有一个△ABC，顶点A、B、C及点O均在格点上，请按要求完成以下操作或运算：
  （1）将△ABC向上平移4个单位，得到△A₁B₁C₁（不写作法，但要标出字母）；
  （2）将△ABC绕点O旋转180°，得到△A₂B₂C₂（不写作法，但要标出字母）；
  （3）求点A绕着点O旋转到点A₂所经过的路径长．
  组卷：821引用：55难度：0.7

  解析

• 22．如图所示的两个图形成中心对称，请你找出对称中心．
  
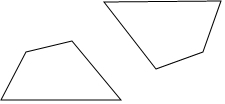  组卷：230引用：2难度：0.9

  解析

• 23．用适当的方法解方程x²-5x+6=0．
  组卷：494引用：22难度：0.3

  解析