2023-2024学年湖北省武汉市江岸区七一华源中学八年级（上）月考数学试卷（9月份）

一、选择题：（共10小题，每题3分，共30分）

• 1．一个三角形的两边长分别为3cm和8cm,则此三角形第三边长可能是（　　）

  A．3cm

  B．5cm

  C．7cm

  D．11cm
  组卷：699引用：20难度：0.9

  解析

• 2．如图，∠ACD=120°，∠B=20°，则∠A的度数是（　　）
  

  A．120°

  B．90°

  C．100°

  D．30°
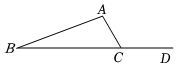  组卷：718引用：16难度：0.7

  解析

• 3．三角形的重心是（　　）

  A．三角形三条边上中线的交点

  B．三角形三条边上高线的交点

  C．三角形三条边垂直平分线的交点

  D．三角形三条内角平分线的交点
  组卷：2095引用：20难度：0.9

  解析

• 4．工人师傅常用角尺平分一个任意角，做法是：如图在∠AOB的边OA、OB上分别取OM=ON，移动角尺，使角尺的两边相同的刻度分别与M、N重合，得到∠AOB的平分线OP，做法中用到三角形全等的判定方法是（　　）

  A．SSS

  B．SAS

  C．ASA

  D．HL
  组卷：6428引用：78难度：0.7

  解析

• 5．六边形共有（　　）条对角线．

  A．7

  B．8

  C．9

  D．10
  组卷：178引用：2难度：0.5

  解析

• 6．已知等腰三角形的周长为18，一边长为4，则它的底边长是（　　）

  A．4

  B．10

  C．4或7

  D．4或10
  组卷：333引用：5难度：0.5

  解析

• 7．如图，AB⊥CD，且AB=CD．E、F是AD上两点，CE⊥AD，BF⊥AD，若CE=6，BF=3，EF=2，则AD的长为（　　）

  A．7

  B．6

  C．5

  D．4
  组卷：1263引用：7难度：0.7

  解析

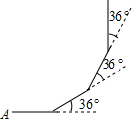• 8．如图，小明从A点出发，沿直线前进10米后向左转36°，再沿直线前进10米，再向左转36°……照这样走下去，他第一次回到出发点A点时，一共走的路程是（　　）

  A．100米

  B．110米

  C．120米

  D．200米
  组卷：1682引用：24难度：0.7

  解析

三、解答题：（共8小题，共72分）

• 23．问题引入：课外兴趣小组活动时，老师提出这样的问题：如图1，在△ABC中，AB=5，AC=3，求BC边上的中线的取值范围．小华在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE，把AB，AC，2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．从中他总结出：解题时，条件中若出现“中线”“中点”等条件，可以考虑将中线加倍延长，构造全等三角形，把分散的条件和需求证的结论集中到同一个三角形中．
  
  （1）请你用小华的方法证明AB+AC＞2AD；
  （2）由第（1）问方法的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的一点，AE是△ABD的中线，CD=AB，∠BDA=∠BAD，求证：AC=2AE；
  （3）如图3，在Rt△ABO和Rt△CDO中，∠AOB=∠COD=90°，OA=OB，OC=OD，连接AD，点M为AD中点，连接OM，请你直接写出

  BC

  OM

  的值．
  组卷：255引用：4难度：0.5

  解析

• 24．已知在平面直角坐标系中，点A的坐标是（0，2），点P是第一象限内一动点．
  （1）①：如图①．若动点P（a,b）满足|3a-9|+（3-b）²=0，且PA⊥PB，求点B的坐标．
  ②：如图②，在第（1）问的条件下，将∠APB逆时针旋转至如图∠CPD所示位置，求OD-OC的值．
  （2）如图③，若点A与点A'关于x轴对称，且BM⊥PA′，若动点P满足∠APA′=2∠OBA'，问：

  P

  A

  ′

  -

  PA

  PM

  的值是否发生变化？若变化，请说明理由，若不变化，请求出其值．
  
  组卷：702引用：3难度：0.1

  解析