2022-2023学年广东省深圳市南山区同乐实验学校九年级(上)期中数学试卷
发布:2024/6/12 8:0:8
一.选择题(每题3分,共30分)
-
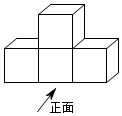 1.如图所示的几何体是由4个相同的小正方体搭成的,它的主视图是( )组卷:79引用:4难度:0.8
1.如图所示的几何体是由4个相同的小正方体搭成的,它的主视图是( )组卷:79引用:4难度:0.8 -
2.我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题:直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.意思是:矩形面积864平方步,宽比长少12步,问宽和长各几步.设长为x步,则可列方程为( )
组卷:385引用:7难度:0.6 -
3.在一个不透明纸箱中放有除数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之积为偶数的概率为( )
组卷:770引用:13难度:0.5 -
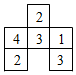 4.如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )组卷:1448引用:16难度:0.6
4.如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )组卷:1448引用:16难度:0.6 -
5.若直角三角形的两边长分别是方程x2-7x+12=0的两根,则该直角三角形的面积是( )
组卷:3520引用:33难度:0.6 -
6.某超市销售一种商品,其进价为每千克30元,按每千克45元出售,每天可售出300千克,为让利于民,超市采取降价措施,当售价每千克降低1元时,每天销量可增加50千克,若每天的利润要达到5500元,则实际售价应定为多少元?设售价每千克降低x元,可列方程为( )
组卷:864引用:4难度:0.6 -
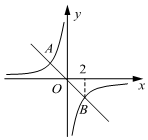 7.如图,正比例函数y1=k1x(k1<0)的图象与反比例函数y2=(k2<0)的图象相交于A,B两点,点B的横坐标为2,当y1>y2时,x的取值范围是( )k2x组卷:3148引用:20难度:0.7
7.如图,正比例函数y1=k1x(k1<0)的图象与反比例函数y2=(k2<0)的图象相交于A,B两点,点B的横坐标为2,当y1>y2时,x的取值范围是( )k2x组卷:3148引用:20难度:0.7
三.解答题(共7小题)
-
21.(1)如图1,将直角三角板的直角顶点放在正方形ABCD上,使直角顶点与D重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.则DP DQ(填“>”“<”或“=”);
(2)将(1)中“正方形ABCD”改成“矩形ABCD”,且AD=2,CD=4,其他条件不变.
①如图2,若PQ=5,求AP长.
②如图3,若BD平分∠PDQ,则DP的长为 .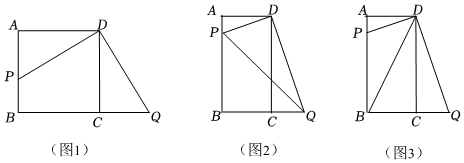 组卷:2689引用:10难度:0.3
组卷:2689引用:10难度:0.3 -
22.(1)【证明体验】如图1,正方形ABCD中,E、F分别是边AB和对角线AC上的点,∠EDF=45°.
①求证:△DBE∼△DCF;
②=;BECF
(2)【思考探究】如图2,矩形ABCD中,AB=6,BC=8,E、F分别是边AB和对角线AC上的点,tan∠EDF=,BE=5,求CF的长;43
(3)【拓展延伸】如图3,菱形ABCD中,BC=5,对角线AC=6,BH⊥AD交DA的延长线于点H,E、F分别是线段HB和AC上的点,tan∠EDF=,HE=34,求CF的长.85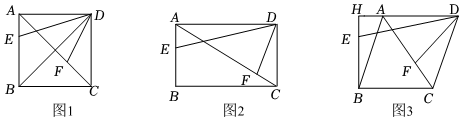 组卷:1734引用:13难度:0.2
组卷:1734引用:13难度:0.2


