2023年贵州省中考数学冲刺试卷（一）

一、单选题（本题共12个小题，每小题3分，共36分）

• 1．-

  2

  3

  的相反数是（　　）

  A． 2 3

  B．- 3 2

  C． 3 2

  D．- 2 3
  组卷：877引用：287难度：0.9

  解析

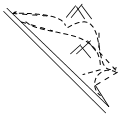• 2．如图，工程队准备将一段笔直的河道改弯，从而增加游览船的航程，让游客饱览山间风光．这其中体现的数学原理是（　　）

  A．两点确定一条直线	B．经过一点有无数条直线
  C．两点之间，线段最短	D．垂线段最短
  组卷：596引用：5难度：0.8

  解析

• 3．在平面直角坐标系中，点P（-3，0）在（　　）

  A．x轴上

  B．y轴上

  C．第三象限

  D．第四象限
  组卷：140引用：5难度：0.9

  解析

• 4．一个几何体的三视图如图所示，那么这个几何体是（　　）

  A．

  B．

  C．

  D．
  组卷：602引用：33难度：0.9

  解析

• 5．随着“一带一路”建设的不断发展，我国已与多个国家建立了经贸合作关系，去年中哈铁路（中国至哈萨克斯坦）运输量达8200000吨，将8200000用科学记数法表示为（　　）

  A．8.2×108

  B．82×108

  C．8.2×106

  D．82×107
  组卷：56引用：4难度：0.8

  解析

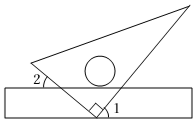• 6．将含30°的直角三角板与直尺如图所示放置，若∠2=40°，则∠1的度数为（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  组卷：582引用：13难度：0.6

  解析

• 7．一组数据x₁，x₂，x₃，x₄，x₅的平均数是x,另一组数据2x₁+5，2x₂+5，2x₃+5，2x₄+5，2x₅+5的平均数是（　　）

  A．x

  B．2x

  C．2x+5

  D．10x+25
  组卷：898引用：10难度：0.9

  解析

• 8．实数a,b,c满足a＞b,且ac＞bc,它们在数轴上的对应点的位置可以是（　　）

  A．	B．
  C．	D．
  组卷：243引用：8难度：0.5

  解析

三、解答题（本题共9个小题，共98分）

• 24．已知二次函数y=a（x+2a-1）（x-a+2）（a是常数，a≠0）．
  （1）当a=1时，求函数的表达式，并写出函数图象的顶点坐标．
  （2）若此函数图象对称轴为直线x=-2时，求函数的最小值．
  （3）设此二次函数的顶点坐标为（m,n），当a≠1时，求证：

  n

  m

  +

  a

  ≤

  9

  8

  ．
  组卷：1375引用：4难度：0.3

  解析

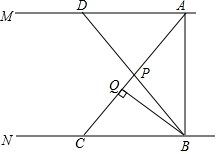• 25．如图，AM∥BN，AB⊥BN，点C在射线BN上且∠ACB=50°，BQ⊥AC于点Q，点P是线段QA上任意一点，延长BP交AM于点D，AB=6．
  （1）若点P为AC中点，求证：△APD≌△CPB；
  （2）当△PBC为等腰三角形时，求∠PBC的度数；
  （3）直接写出△PBC的外心运动的路径长．
  组卷：103引用：2难度：0.5

  解析