2022-2023学年北京市海淀区建华实验学校九年级（上）第二次月考数学试卷

一、选择题（本题共16分，每小题2分）

• 1．下列四个图形中，是中心对称图形的是（　　）

  A．	B．
  C．	D．
  组卷：480引用：27难度：0.9

  解析

• 2．将抛物线y=3x²向左平移2个单位后得到新的抛物线的表达式为（　　）

  A．y=3x2+2

  B．y=3x2-2

  C．y=3（x+2）2

  D．y=3（x-2）2
  组卷：185引用：3难度：0.8

  解析

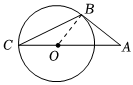• 3．如图，AB切⊙O于点B，延长AO交⊙O于点C，连接BC．若∠A=40°，则∠C=（　　）

  A．20°

  B．25°

  C．40°

  D．50°
  组卷：194引用：8难度：0.9

  解析

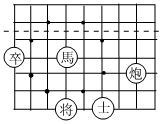• 4．中国象棋文化历史久远，在图中所示的部分棋盘中，“馬”的位置在“…”（图中虚线）的下方，“馬”移动一次能够到达的所有位置已用“●”标记，则“馬”随机移动一次，到达的位置在“…”上方的概率是（　　）

  A． 1 2

  B． 1 4

  C． 1 6

  D． 1 8
  组卷：307引用：6难度：0.6

  解析

• 5．参加一次活动的每个人都和其他人各握了一次手，所有人共握手10次，有多少人参加活动？设有x人参加活动，可列方程为（　　）

  A． 1 2 x（x-1）=10	B．x（x-1）=10
  C． 1 2 x（x+1）=10	D．2x（x-1）=10
  组卷：2063引用：18难度：0.6

  解析

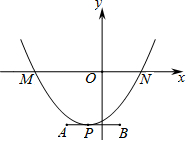• 6．如图，一条抛物线与x轴相交于M，N两点（点M在点N的左侧），其顶点P在线段AB上移动，点A，B的坐标分别为（-2，-3），（1，-3），点N的横坐标的最大值为4，则点M的横坐标的最小值为（　　）

  A．-1

  B．-3

  C．-5

  D．-7
  组卷：1355引用：11难度：0.4

  解析

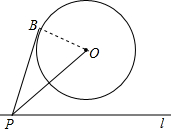• 7．如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点．若PB切⊙O于点B，则PB的最小值是（　　）

  A． 13

  B． 5

  C．3

  D．2
  组卷：878引用：19难度：0.9

  解析

• 8．已知二次函数y=ax²+bx+c,当-1≤x≤1时，总有-1≤y≤1，有如下几个结论：
  ①当b=c=0时，|a|≤1；
  ②当a=1时，c的最大值为0；
  ③当x=2时，y可以取到的最大值为7．
  上述结论中，所有正确结论的序号是（　　）

  A．①②

  B．①③

  C．②③

  D．①②③
  组卷：974引用：4难度：0.2

  解析

二、填空题（本题共16分，每小题2分）

• 9．若代数式

  1

  x

  -

  1

  有意义，则实数x的取值范围是

  ．
  组卷：1928引用：42难度：0.9

  解析

三、解答题（共68分，17题8分，18-25每题5分，26题6分，27，28各7分）

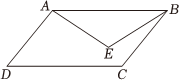• 27．在平行四边形ABCD内有一点E，使得AE=BE=AD，作点E关于直线AB的对称点F，连接DE，CF．
  （1）依题补全图形；
  （2）若∠DAE=α，求∠BCF的大小（用含有α的式子表示）；
  （3）用等式表示线段AD，DE和CF之间的数量关系，并证明．
  组卷：34引用：2难度：0.5

  解析

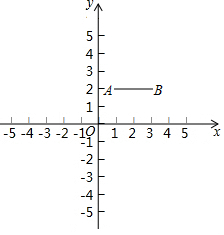• 28．如图，在平面直角坐标系xOy中，已知点A（1，2），B（3，2），连接AB．若对于平面内一点P，线段AB上都存在点Q，使得PQ≤1，则称点P是线段AB的“临近点”．
  （1）在点C（0，2），D（2，

  3

  2

  ），E（4，1）中，线段
  AB的“临近点”是

  ；
  （2）若点M（m,n）在直线y=-

  3

  3

  x+2上，且是线段AB的“临近点”，求m的取值范围；
  （3）若直线y=-

  3

  3

  x+b上存在线段AB的“临近点”，求b的取值范围．
  组卷：601引用：3难度：0.3

  解析