2022-2023学年吉林省长春市东北师大东安实验学校九年级（上）第一次质检数学试卷

一、选择题（每小题3分，共24分）

• 1．2018年一季度，华为某地销售公司营收入比2017年同期增长22%，2019年第一季度营收入比2018年同期增长30%，设2018年和2019年第一季度营收入的平均增长率为x,则可列方程（　　）

  A．2x=22%+30%

  B．（1+x）2=1+22%+30%

  C．1+2x=（1+22%）（1+30%）

  D．（1+x）2=（1+22%）（1+30%）
  组卷：450引用：3难度：0.8

  解析

• 2．如图，小卓利用标杆EF测量旗杆AB的高度，测得小桌的身高CD=1.8米，标杆EF=2.4米，DF=1米，BF=11米，则旗杆AB的高度是（　　）

  A．6.4米

  B．7.2米

  C．9米

  D．9.6米
  组卷：127引用：1难度：0.7

  解析

• 3．解下面方程：（1）（x-2）²=5，（2）x²-3x-2=0，（3）x²+x-6=0，较适当的方法分别为（　　）

  A．（1）直接开平方法（2）因式分解法（3）配方法

  B．（1）因式分解法（2）公式法（3）直接开平方法

  C．（1）公式法（2）直接开平方法（3）因式分解法

  D．（1）直接开平方法（2）公式法（3）因式分解法
  组卷：193引用：17难度：0.9

  解析

• 4．式子

  x

  -

  1

  在实数范围内有意义，则x的取值范围是（　　）

  A．x＞-1

  B．x≥1

  C．x≥2

  D．x＜3
  组卷：160引用：3难度：0.9

  解析

• 5．如图，△ABC与△DEF位似，点O为位似中心，已知OA：OD=1：3，且△ABC的面积为4，则△DEF的面积为（　　）

  A．8

  B．10

  C．16

  D．36
  组卷：144引用：2难度：0.7

  解析

• 6．已知

  b

  a

  =5，则

  a

  -

  b

  a

  +

  b

  的值是（　　）

  A． - 2 3

  B．- 1 3

  C． 2 3

  D． 1 3
  组卷：1127引用：9难度：0.7

  解析

• 7．下列两个三角形不一定相似的是（　　）

  A．两个等边三角形	B．两个全等三角形
  C．两个直角三角形	D．两个等腰直角三角形
  组卷：131引用：2难度：0.9

  解析

• 8．一元二次方程x²-6x=-9的根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．没有实数根	D．无法确定
  组卷：138引用：4难度：0.7

  解析

二、填空题（每小题3分，共18分）

• 9．如图，在△ABC中，D，E分别是AB，BC上的点，且DE∥AC，AE，CD交于点F，若S_△BDE：S_△DEC=1：3，则S_△DEF：S_△AFC=

   

  ．
  组卷：418引用：3难度：0.7

  解析

• 10．计算：

  12

  6

  =

  ．
  组卷：504引用：6难度：0.9

  解析

• 11．有一人患了流感，经过两轮传染后共有100人患了流感，那么每轮传染中平均一个人传染给

  个人．
  组卷：534引用：32难度：0.9

  解析

• 12．如图，ABCD是正方形，E、F是AB、BC的中点，连接CC交DB、DF于G、H，则EG：GH=

   

  ．
  组卷：279引用：1难度：0.7

  解析

• 13．已知x²+ax-12=0能分解成两个整系数的一次因式的乘积，则符合条件的整数a的个数为

   

  ．
  组卷：137引用：2难度：0.7

  解析

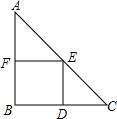• 14．如图，在Rt△ABC中，AB=BC，∠B=90°，AC=10

  2

  ．四边形BDEF是△ABC的内接正方形（点D、E、F在三角形的边上）．则此正方形的面积是

  ．
  组卷：2057引用：60难度：0.7

  解析

三、解答题（本大题共10小题，共78分）

• 15．计算：

  16

  ÷

  2

  -

  1

  3

  ×

  6

  ．
  组卷：360引用：1难度：0.6

  解析

• 16．设x₁，x₂是关于x的方程x²-4x+k+1=0的两个实数根．试问：是否存在实数k,使得x₁•x₂＞x₁+x₂成立？请说明理由．
  （温馨提示：关于x的一元二次方程ax²+bx+c=0（a≠0），当b²-4ac≥0时，则它的两个实数根是：

  x

  1

  ，

  2

  =

  -

  b

  ±

  b

  2

  -

  4

  ac

  2

  a

  ）
  组卷：108引用：14难度：0.5

  解析

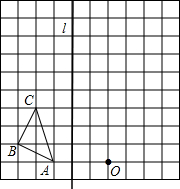• 17．如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A₁B₁C₁和△A₂B₂C₂；
  （1）先作△ABC关于直线l成轴对称的图形，再向上平移1个单位，得到△A₁B₁C₁；
  （2）以图中的O为位似中心，将△A₁B₁C₁作位似变换且放大到原来的两倍，得到△A₂B₂C₂．
  组卷：208引用：14难度：0.7

  解析

• 18．如图1，在△ABC中，∠A=120°，AB=AC，点D、E分别在边AB、AC上，AD=AE，连接BE，点M、N、P分别为DE、BE、BC的中点，连接NM、NP．
  （1）图1中，线段NM、NP的数量关系是

  ，∠MNP的度数为

  ；
  （2）将△ADE绕点A顺时针旋转到如图2所示的位置，连接MP，你认为△NMP是什么特殊三角形，请写出你的猜想并证明你的结论；
  （3）把△ADE绕点A在平面内旋转，若AD=3，AB=5，请写出△MNP面积的最大值．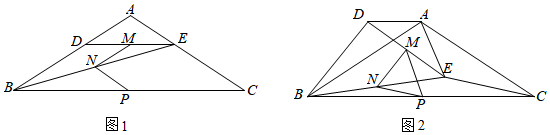
  
  组卷：379引用：1难度：0.3

  解析

• 19．在△ABC中，E，F是BC边上的两个三等分点，BM是AC边上的中线，AE，AF分别与BM交于D，G．求：BD：DG：GM．
  组卷：47引用：1难度：0.6

  解析

• 20．已知在Rt△ABC中，CD⊥AB于点D．
  
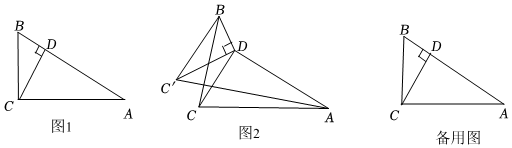
  （1）在图1中，写出其中两对相似三角形．
  （2）已知BD=1，DC=2，将△CBD绕着点D按顺时针方向进行旋转得到△C'BD，连接AC'，BC．
  ①如图2，判断AC'与BC之间的位置及数量关系，并证明；
  ②在旋转过程中，当点A，B，C'在同一直线时，求BC的长．
  组卷：1034引用：3难度：0.3

  解析

• 21．直播购物逐渐走进了人们的生活．某电商在抖音上对一款成本价为40元的小商品进行直播销售，如果按每件60元销售，每天可卖出20件．通过市场调查发现，每件小商品售价每降低5元，日销售量增加10件．
  （1）若日利润保持不变，商家想尽快销售完该款商品，每件售价应定为多少元？
  （2）小明的线下实体商店也销售同款小商品，标价为每件62.5元．为提高市场竞争力，促进线下销售，小明决定对该商品实行打折销售，使其销售价格不超过（1）中的售价，则该商品至少需打几折销售？
  组卷：8167引用：50难度：0.5

  解析

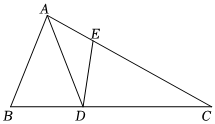• 22．如图，在△ABC中，点D在BC边上，AD=AB，点E在AC边上，且∠DEC=∠ADB．求证：AB²=AE•AC．
  组卷：367引用：1难度：0.7

  解析

• 23．阅读下面提供的内容：
  关于x的一元二次方程ax²+bx+c=0（a≠0），如果a+b+c=0，那么它的两根分别为x₁=1，x₂=

  c

  a

  ．
  证明：因为a+b+c=0，所以c=-a-b,将c=-a-b代入ax²+bx+c=0，得ax²+bx-a-b=0，即a（x²-1）+b（x-1）=0，所以（x-1）（ax+a+b）=0，所以x₁=1，x₂=

  -

  a

  -

  b

  a

  =

  c

  a

  ．
  （1）请利用上面推导的结论，快速求解下列方程：
  ①5x²-4x-1=0，x₁=

   

  ，x₂=

   

  ；
  ②.5x²+4x-9=0，x₁=

   

  ，x₂=

   

  ；
  ③

  x

  2

  -

  （

  2

  -

  1

  ）

  x

  -

  2

  +

  2

  =

  0

  ，x₁=

   

  ，x₂=

   

  ；
  （2）请写出两个一元二次方程，使它们都有一个根为1．
  组卷：765引用：2难度：0.3

  解析

• 24．解方程：x²-4|x|+4=16．
  组卷：43引用：1难度：0.9

  解析