当前位置：试卷中心 > 试卷详情

2022-2023学年甘肃省兰州市城关区树人中学八年级（下）期末数学试卷

发布：2025/11/6 14:0:39

一、选择题（每小题3分，共36分）

1．如图，在▱ABCD中，CD=4，∠B=60°，BE：EC=2：1，依据尺规作图的痕迹，则▱ABCD的面积为（　　）
A．12 B．12
2
C．12
3
D．12
5
组卷：834引用：10难度：0.5
2．若式子
x
x
-
1
有意义，则x的取值范围是（　　）
A．x≠-1 B．x≠1 C．x＞1 D．x≠0
组卷：61引用：4难度：0.9
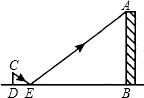3．如图，王华在地面上放置一个平面镜E来测量铁塔AB的高度，镜子与铁塔的距离EB=20米，镜子与王华的距离ED=2米时，王华刚好从镜子中看到铁塔顶端点A，已知王华的眼睛距地面的高度CD=1.5米，则铁塔AB的高度是（　　）
A．15米 B．
80
3
米 C．16米 D．16.5米
组卷：255引用：25难度：0.9
4．若一个正多边形的每一个外角都等于40°，则这个正多边形的边数是（　　）
A．7 B．8 C．9 D．10
组卷：3513引用：52难度：0.9
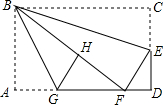5．如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，①∠EBG=45°；②△DEF∽△ABG；③S_△ABG=
3
2
S_△FGH；④AG+DF=FG．则下列结论正确的有（　　）
A．①②④ B．①③④ C．②③④ D．①②③
组卷：518引用：5难度：0.7
6．若m＜n,则下列各式中正确的是（　　）
A．-3m＜-3n B．m+1＜n+1 C．3m＞3n D．m-1＞n-1
组卷：64引用：5难度：0.9
7．下列各式从左到右的变形一定正确的是（　　）
A．
n
m
=
n
+
2
m
+
2
B．
x
2
-
y
2
x
-
y
=x-y
C．
b
a
=
bc
ac
D．
b
a
=
ab
a
2
组卷：81引用：1难度：0.7
8．下列各组图形可以通过平移一个图形得到另一个图形的是（　　）
A． B． C． D．
组卷：60引用：5难度：0.6
9．下列智能手机的功能图标中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：5引用：3难度：0.9
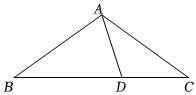10．如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（　　）
A．30° B．36° C．40° D．45°
组卷：4920引用：122难度：0.9
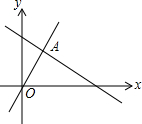11．如图，函数y=2x和y=ax+4的图象相交于点A（m,3），则不等式2x＜ax+4的解集为（　　）
A．x＞
3
2
B．x＞3 C．x＜3 D．x＜
3
2
组卷：1024引用：14难度：0.7
12．如图，矩形ABCD中，已知AB=6，BC=8，点E是边AD上一点，以CE为直角边在与点D的同侧作等腰直角△CEG，连接BG，当点E在边AD上运动时，线段BG长度的最小值是（　　）
A．2
29
B．10
2
C．10
3
D．14
组卷：509引用：2难度：0.9

二、填空题（每小题3分，共12分）

13．不等式组
3
x
-
2
＞
0
x
+
2
＜
4
的解集是

．
组卷：713引用：11难度：0.5
14．▱ABCD的对角线AC、BD相交于点O，BC=8，AC=6，BD=12，则△AOD的周长为
．
组卷：51引用：2难度：0.7
15．因式分解：x³y²-x³=
．
组卷：711引用：7难度：0.5
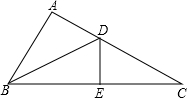16．如图，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，若AD=2cm,则CD=
cm.
组卷：22引用：11难度：0.7

三、解答题（共72分）

17．增根是在分式方程转化为整式方程的过程中产生的，分式方程的增根，不是分式方程的根，而是该分式方程化成的整式方程的根，所以涉及分式方程的增根问题的解题步骤通常为：①去分母，化分式方程为整式方程；②将增根代入整式方程中，求出方程中字母系数的值．
阅读以上材料后，完成下列探究：
探究1：m为何值时，方程
3
x
x
-
3
+5=
m
3
-
x
有增根．
探究2：m为何值时，方程
3
x
x
-
3
+5=
m
3
-
x
的根是-1．
探究3：任意写出三个m的值，使对应的方程
3
x
x
-
3
+5=
m
3
-
x
的三个根中两个根之和等于第三个根；
探究4：你发现满足“探究3”条件的m₁、m₂、m₃的关系是

．
组卷：924引用：1难度：0.5
18．计算：
（1）（
1
4
+
3
8
-
7
12
）÷
1
24
；
（2）-2³÷8-
1
4
×（-2）²；
（3）-2⁴+（3-7）²-2×（-1）²；
（4）[（-2）³+
4
3
]÷4+（-
2
3
）．
组卷：1321引用：2难度：0.8
19．为全力助推九龙华岩板块建设，大力发展美丽的新华岩，现招标建设某全长480米绿化带，A，B两个工程队的竞标，A队平均每天绿化长度是B队的2倍，若由一个工程队单独完成绿化，B队比A队要多用8天，
（1）分别求出A，B两队平均每天绿化长度．
（2）若决定由两个工程队共同合作绿化，要求至多7天完成绿化任务，两队都按（1）中的工作效率绿化完2天时，现又多出180米需要绿化，为了不超过7天时限，两队决定从第3天开始，各自都提高工作效率，且A队平均每天绿化长度仍是B队的2倍，则A队提高工作效率后平均每天至少绿化多少米？
组卷：1808引用：3难度：0.1
20．一个四位正整数A的千位上的数字小于十位上的数字，且千位上的数字与百位上的数字之和等于十位上的数字与个位上的数字之和，均等于10，则称A为“十全十美数”，将“十全十美数”A的千位和百位数字组成的两位数与十位和个位数字组成的两位数的和记为F（A），将“十全十美数”A的千位和十位数字组成的两位数与百位和个位数字组成的两位数的差记为G（A）．
例如：四位正整数2873，
∵2+8=7+3=10，且2＜7
∴2873是“十全十美数”，
此时，F（A）=28+73=101，G（A）=27-83=-56．
（1）若M是最大的“十全十美数”，请直接写出：M=
，F（M）=
，G（M）=
；
（2）若A是“十全十美数”，且2F（A）+G（A）能被9整除，求所有符合条件的A的值．
组卷：406引用：2难度：0.5
21．将一块长方体蛋糕平均分成3份，若按照如图1方式进行分割，每份的蛋糕胚一样多，但奶油不一样多（①和③奶油多，②奶油少），那么如何分割，才能使得3份的蛋糕胚和奶油一样多呢？如图2，首先我们可以将蛋糕抽象成矩形，用加粗线条表示有奶油的边，然后将矩形沿其对角线分割并拼成如图3的平行四边形ABCD，分别取边AB、CD的三等分点E、F和G、H，如图4，按EG、FH分割成3份（Ⅰ，Ⅱ，Ⅲ），此种分法能够保证每份的蛋糕坯一样多，奶油是否一样多，我们只需判断每份中加粗线条的长度和是否相等，请你给出判断并加以证明．
组卷：143引用：2难度：0.7
22．已知关于x,y的方程组
3
x
+
y
=
2
k
+
1
x
-
y
=
6
k
-
5
的解是非负数．
（1）求k的取值范围；
（2）化简：|2k+3|-|k-2|．
组卷：132引用：2难度：0.6
23．（1）解不等式：
5
x
+
3
2
-
2
x
-
4
3
≥
1
，并把它的解集在数轴上表示出来．

（2）解不等式组
x
-
2
＜
4
（
x
+
1
）
①
x
-
1
2
≤
1
②
，并写出该不等式组的所有整数解．
组卷：162引用：3难度：0.7
24．化简：
x
2
-
2
x
x
2
-
x
÷
（
3
x
-
1
-
x
-
1
）
．
组卷：567引用：1难度：0.5
25．如图，△ABC中，∠ABC=90°，AB=
1
2
AC，求证：∠C=30°．
组卷：118引用：2难度：0.7
26．如图，在△ABC中，AD⊥BC，垂足为D，EC⊥AB，垂足为E，连接DE．试说明△BDE∽△BAC．
组卷：556引用：4难度：0.5
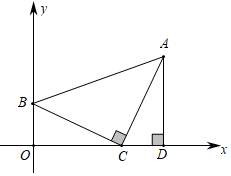27．如图，等腰直角△ABC中，BC=AC，∠ACB=90°，现将该三角形放置在平面直角坐标系中，点B坐标为（0，2），点C坐标为（6，0）．
（1）过点A作AD⊥x轴，求OD的长及点A的坐标；
（2）连接OA，若P为坐标平面内不同于点A的点，且以O、P、C为顶点的三角形与△OAC全等，请直接写出满足条件的点P的坐标；
（3）已知OA=10，试探究在x轴上是否存在点Q，使△OAQ是以OA为腰的等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
组卷：199引用：4难度：0.2
28．如图，△ABC中，AB=AC=5，BC=6，AD平分∠BAC交BC于点D，分别以点A和点C为圆心，大于
1
2
AC的长为半径作弧，两弧相
交于点M和点N，连接MN，交AD于点E，求AE的长．
组卷：199引用：3难度：0.6

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． n m = n + 2 m + 2	B． x 2 - y 2 x - y =x-y
C． b a = bc ac	D． b a = ab a 2

x - 2 ＜ 4 （ x + 1 ）	①
x - 1 2 ≤ 1	②

2022-2023学年甘肃省兰州市城关区树人中学八年级（下）期末数学试卷

一、选择题（每小题3分，共36分）

1．如图，在▱ABCD中，CD=4，∠B=60°，BE：EC=2：1，依据尺规作图的痕迹，则▱ABCD的面积为（ ）

2．若式子xx-1有意义，则x的取值范围是（ ）

3．如图，王华在地面上放置一个平面镜E来测量铁塔AB的高度，镜子与铁塔的距离EB=20米，镜子与王华的距离ED=2米时，王华刚好从镜子中看到铁塔顶端点A，已知王华的眼睛距地面的高度CD=1.5米，则铁塔AB的高度是（ ）

4．若一个正多边形的每一个外角都等于40°，则这个正多边形的边数是（ ）

6．若m＜n,则下列各式中正确的是（ ）

7．下列各式从左到右的变形一定正确的是（ ）

8．下列各组图形可以通过平移一个图形得到另一个图形的是（ ）

9．下列智能手机的功能图标中，既是轴对称图形又是中心对称图形的是（ ）

10．如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（ ）

11．如图，函数y=2x和y=ax+4的图象相交于点A（m,3），则不等式2x＜ax+4的解集为（ ）

12．如图，矩形ABCD中，已知AB=6，BC=8，点E是边AD上一点，以CE为直角边在与点D的同侧作等腰直角△CEG，连接BG，当点E在边AD上运动时，线段BG长度的最小值是（ ）

二、填空题（每小题3分，共12分）

13．不等式组3x-2＞0x+2＜4的解集是 ．

14．▱ABCD的对角线AC、BD相交于点O，BC=8，AC=6，BD=12，则△AOD的周长为 ．

15．因式分解：x3y2-x3=．

16．如图，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，若AD=2cm,则CD=cm.

三、解答题（共72分）

18．计算：（1）（14+38-712）÷124；（2）-23÷8-14×（-2）2；（3）-24+（3-7）2-2×（-1）2；（4）[（-2）3+43]÷4+（-23）．

22．已知关于x,y的方程组3x+y=2k+1x-y=6k-5的解是非负数．（1）求k的取值范围；（2）化简：|2k+3|-|k-2|．

23．（1）解不等式：5x+32-2x-43≥1，并把它的解集在数轴上表示出来．（2）解不等式组x-2＜4（x+1）①x-12≤1②，并写出该不等式组的所有整数解．

24．化简：x2-2xx2-x÷（3x-1-x-1）．

25．如图，△ABC中，∠ABC=90°，AB=12AC，求证：∠C=30°．

26．如图，在△ABC中，AD⊥BC，垂足为D，EC⊥AB，垂足为E，连接DE．试说明△BDE∽△BAC．

28．如图，△ABC中，AB=AC=5，BC=6，AD平分∠BAC交BC于点D，分别以点A和点C为圆心，大于12AC的长为半径作弧，两弧相交于点M和点N，连接MN，交AD于点E，求AE的长．

1．如图，在▱ABCD中，CD=4，∠B=60°，BE：EC=2：1，依据尺规作图的痕迹，则▱ABCD的面积为（　　）

2．若式子
x
x
-
1
有意义，则x的取值范围是（　　）

3．如图，王华在地面上放置一个平面镜E来测量铁塔AB的高度，镜子与铁塔的距离EB=20米，镜子与王华的距离ED=2米时，王华刚好从镜子中看到铁塔顶端点A，已知王华的眼睛距地面的高度CD=1.5米，则铁塔AB的高度是（　　）

4．若一个正多边形的每一个外角都等于40°，则这个正多边形的边数是（　　）

6．若m＜n,则下列各式中正确的是（　　）

7．下列各式从左到右的变形一定正确的是（　　）

8．下列各组图形可以通过平移一个图形得到另一个图形的是（　　）

9．下列智能手机的功能图标中，既是轴对称图形又是中心对称图形的是（　　）

10．如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（　　）

11．如图，函数y=2x和y=ax+4的图象相交于点A（m,3），则不等式2x＜ax+4的解集为（　　）

12．如图，矩形ABCD中，已知AB=6，BC=8，点E是边AD上一点，以CE为直角边在与点D的同侧作等腰直角△CEG，连接BG，当点E在边AD上运动时，线段BG长度的最小值是（　　）

13．不等式组
3
x
-
2
＞
0
x
+
2
＜
4
的解集是

．

14．▱ABCD的对角线AC、BD相交于点O，BC=8，AC=6，BD=12，则△AOD的周长为
．

15．因式分解：x³y²-x³=
．

16．如图，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，若AD=2cm,则CD=
cm.

18．计算：
（1）（
1
4
+
3
8
-
7
12
）÷
1
24
；
（2）-2³÷8-
1
4
×（-2）²；
（3）-2⁴+（3-7）²-2×（-1）²；
（4）[（-2）³+
4
3
]÷4+（-
2
3
）．

22．已知关于x,y的方程组
3
x
+
y
=
2
k
+
1
x
-
y
=
6
k
-
5
的解是非负数．
（1）求k的取值范围；
（2）化简：|2k+3|-|k-2|．

23．（1）解不等式：
5
x
+
3
2
-
2
x
-
4
3
≥
1
，并把它的解集在数轴上表示出来．

（2）解不等式组
x
-
2
＜
4
（
x
+
1
）
①
x
-
1
2
≤
1
②
，并写出该不等式组的所有整数解．

24．化简：
x
2
-
2
x
x
2
-
x
÷
（
3
x
-
1
-
x
-
1
）
．

25．如图，△ABC中，∠ABC=90°，AB=
1
2
AC，求证：∠C=30°．

28．如图，△ABC中，AB=AC=5，BC=6，AD平分∠BAC交BC于点D，分别以点A和点C为圆心，大于
1
2
AC的长为半径作弧，两弧相
交于点M和点N，连接MN，交AD于点E，求AE的长．