当前位置：试卷中心 > 试卷详情

2023年湖北省潜江市、天门市中考数学模拟试卷（四）

发布：2025/11/6 2:0:8

一、选择题（本大题共10个小题，每小题3分，满分30分，在下列每个小题给出的四个答案中有且只有一个正确答案，请将正确答案的字母代号在答题卡上涂黑，涂错或不涂均为零分）

1．下列事件：
①在足球赛中，弱队战胜强队．
②抛掷1枚硬币，硬币落地时正面朝上．
③任取两个正整数，其和大于1
④长为3cm,5cm,9cm的三条线段能围成一个三角形．
其中确定事件有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：1876引用：66难度：0.7
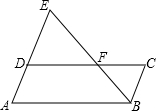2．如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（　　）
A．
ED
EA
=
DF
AB
B．
DE
CB
=
EF
FB
C．
BF
BE
=
BC
AE
D．
BC
DE
=
BF
BE
组卷：582引用：12难度：0.7
3．设a、b为x²+x-2011=0的两个实根，则a³+a²+3a+2014b=（　　）
A．2014 B．-2014 C．2011 D．-2011
组卷：927引用：5难度：0.8
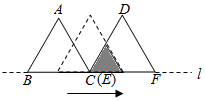4．如图，△ABC和△DEF都是边长为2的等边三角形，它们的边BC，EF在同一条直线l上，点C，E重合．现将△ABC沿着直线l向右移动，直至点B与F重合时停止移动．在此过程中，设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为（　　）
A． B．
C． D．
组卷：5448引用：56难度：0.5
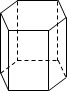5．如图，下列选项中不是正六棱柱三视图的是（　　）
A． B． C． D．
组卷：312引用：64难度：0.7
6．如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合），OD⊥BC，OE⊥AC，垂足分别为D、E，在点C的运动过程中，下列说法正确的是（　　）
A．扇形AOB的面积为
π
2
B．弧BC的长为
π
2
C．∠DOE=30° D．线段DE的长是
2
组卷：74引用：1难度：0.4
7．下列各组数中，相等的是（　　）
A．（-5）²与-5² B．|-5|²与-5²
C．（-7）³ 与-7³ D．|-7|³与-7³
组卷：35引用：3难度：0.9
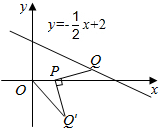8．如图，在平面直角坐标系中，Q是直线y=-
1
2
x+2上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q'，连接OQ'，则OQ'的最小值为（　　）
A．
4
5
5
B．
5
C．
5
2
3
D．
6
5
5
组卷：5479引用：37难度：0.6
9．计算：（-2a³）²的结果是（　　）
A．2a⁶ B．4a⁶ C．-4a⁶ D．4a⁵
组卷：578引用：3难度：0.9
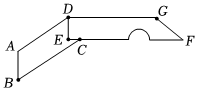10．如图，小刀的刀柄DEFG是一个直角梯形（挖去一个半圆），刀片上下两边AD和BC平行，转动刀片到如图所示的位置，则∠ADE+∠BCE的度数为（　　）
A．60° B．80° C．90° D．120°
组卷：128引用：3难度：0.7

二、填空题（本大题共5个小题，每小题3分，满分15分，请将答案直接填写在答题卡对应的横线上）

11．有两组卡片，第一组卡片上分别写有数字“2，3，4”，第二组卡片上分别写有数字“3，4，5”，现从每组卡片中各随机抽出一张，用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字，差为负数的概率为

．
组卷：289引用：67难度：0.5
12．如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D，过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE，对于下列结论：①AD=DC；②△CBA∽△CDE；③
ˆ
BD
=
ˆ
AD
；④AE为⊙O的切线，一定正确的结论选项是

．
组卷：477引用：6难度：0.7
13．2019年4月10日，全球六地同步发布“事件视界望远镜”获取的首张“黑洞”照片，这个位于室女座足系团中的黑洞，质量约为太阳的6500000000倍．将6500000000用科学记数法表示为
．
组卷：75引用：2难度：0.9
14．某船在河中航行，已知顺流速度是14km/h,逆流速度是8km/h,那么它在静水中的速度是
km/h,水流速度是
km/h.
组卷：81引用：2难度：0.9
15．如图所示，在某一电路中，保持电压不变，电阻R（欧）与电流I（安）之间的函数关系式是
．
组卷：124引用：4难度：0.6

三、解答题（本大题共9个题，满分63分）

16．反比例函数y=
1
x
和y=
k
x
（k≠0）在第一象限内的图象如图所示，点P在y=
k
x
的图象上，PC⊥x轴，垂足为C，交y=
1
x
的图象于点A，PD⊥y轴，垂足为D，交y=
1
x
的图象于点B．已知点A（m,1）为线段PC的中点．
（1）求m和k的值；
（2）求四边形OAPB的面积．
组卷：1864引用：54难度：0.5
17．阅读材料：
关于x的方程：x+
1
x
=c+
1
c
的解是x₁=c,x₂=
1
c
；
x
-
1
x
=c
-
1
c
（既x+
-
1
x
=c+
-
1
c
）的解是x₁=c,x₂=
-
1
c
；
x+
2
x
=c+
2
c
的解是x₁=c,x₂=
2
c
；
x+
3
x
=c+
3
c
的解是x₁=c,x₂=
3
c
；
…
（1）请观察上述方程与解的特征，比较关于x的方程x+
m
x
=a+
m
a
（m≠0）与它们的关系，猜想它的解是什么，并利用“方程的解”的概念进行验证：
（2）由上述的观察、比较、猜想、验证，可以得出结论：如果方程左边是未知数与其倒数的倍数的和，方程右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解，请用这个结论解下面关于x的方程（直接写出答案）；
①x+
3
x
+
1
=4+
3
5
；
②x+
4
x
-
1
=a+
4
a
-
1
．
组卷：622引用：2难度：0.8
18．如图所示，甲、乙两同学分别住在秀水大道两旁的A，B处，一天其中一人要到对方家中去复习功课，为了能最快速度到达，如何走最近？画图说明．
组卷：2引用：1难度：0.5
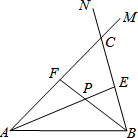19．在线段AB的同侧作射线AM和BN，若∠MAB与∠NBA的平分线分别交射线BN，AM于点E，F，AE和BF交于点P．如图，点点同学发现当射线AM，BN交于点C；且∠ACB=60°时，有以下两个结论：
①∠APB=120°；②AF+BE=AB．
那么，当AM∥BN时：
（1）点点发现的结论还成立吗？若成立，请给予证明；若不成立，请求出∠APB的度数，写出AF，BE，AB长度之间的等量关系，并给予证明；
（2）设点Q为线段AE上一点，QB=5，若AF+BE=16，四边形ABEF的面积为32
3
，求AQ的长．
组卷：2348引用：4难度：0.1
20．如图①，在平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（4，0）、（4，3），点P为OA边上一个动点，PQ⊥OA于P，交OB于点Q，过Q点作QR⊥AB于R，设OP=x,四边形PQRA的面积为S．
（1）求S与x之间的函数关系式．
（2）当x取何值时四边形PQRA的面积最大．
（3）如图②，若点P从O点出发，沿OA运动，每秒1个单位长度，点M从B点出发，沿BO运动，每秒2个单位长度，当其中一个点到达终点，另一个点也同时停止运动，连接PM，则当运动时间t取何值时，△OPM为等腰三角形．
组卷：134引用：3难度：0.1
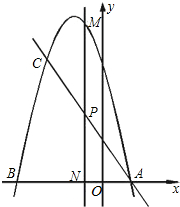21．如图，抛物线y=a（x+3）（x-1）与x轴相交于A、B两点（点A在点B右侧），过点A的直线交抛物线于另一点C，点C的坐标为（-2，6）．
（1）求a的值及直线AC的函数关系式；
（2）P是线段AC上一动点，过点P作y轴的平行线，交抛物线于点M，交x轴于点N．
①求线段PM长度的最大值；
②在抛物线上是否存在这样的点M，使得△CMP与△APN相似？如果存在，请直接写出所有满足条件的点M的坐标（不必写解答过程）；如果不存在，请说明理由．
组卷：453引用：19难度：0.5
22．已知某商品的进价为每件40元．现在的售价是每件60元．每星期可卖出300件．市场调查反映：如调整价格，每涨价一元．每星期要少卖出10件；每降价一元，每星期可多卖出18件．如何定价才能使利润最大？
组卷：173引用：4难度：0.6

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．扇形AOB的面积为 π 2	B．弧BC的长为 π 2
C．∠DOE=30°	D．线段DE的长是 2

A．（-5）²与-5²	B．\|-5\|²与-5²
C．（-7）³ 与-7³	D．\|-7\|³与-7³

A．	B．
C．	D．

2023年湖北省潜江市、天门市中考数学模拟试卷（四）

一、选择题（本大题共10个小题，每小题3分，满分30分，在下列每个小题给出的四个答案中有且只有一个正确答案，请将正确答案的字母代号在答题卡上涂黑，涂错或不涂均为零分）

1．下列事件：①在足球赛中，弱队战胜强队．②抛掷1枚硬币，硬币落地时正面朝上．③任取两个正整数，其和大于1④长为3cm,5cm,9cm的三条线段能围成一个三角形．其中确定事件有（ ）

2．如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（ ）

3．设a、b为x2+x-2011=0的两个实根，则a3+a2+3a+2014b=（ ）

5．如图，下列选项中不是正六棱柱三视图的是（ ）

6．如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合），OD⊥BC，OE⊥AC，垂足分别为D、E，在点C的运动过程中，下列说法正确的是（ ）

7．下列各组数中，相等的是（ ）

8．如图，在平面直角坐标系中，Q是直线y=-12x+2上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q'，连接OQ'，则OQ'的最小值为（ ）

9．计算：（-2a3）2的结果是（ ）

10．如图，小刀的刀柄DEFG是一个直角梯形（挖去一个半圆），刀片上下两边AD和BC平行，转动刀片到如图所示的位置，则∠ADE+∠BCE的度数为（ ）

二、填空题（本大题共5个小题，每小题3分，满分15分，请将答案直接填写在答题卡对应的横线上）

11．有两组卡片，第一组卡片上分别写有数字“2，3，4”，第二组卡片上分别写有数字“3，4，5”，现从每组卡片中各随机抽出一张，用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字，差为负数的概率为 ．

12．如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D，过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE，对于下列结论：①AD=DC；②△CBA∽△CDE；③ˆBD=ˆAD；④AE为⊙O的切线，一定正确的结论选项是 ．

13．2019年4月10日，全球六地同步发布“事件视界望远镜”获取的首张“黑洞”照片，这个位于室女座足系团中的黑洞，质量约为太阳的6500000000倍．将6500000000用科学记数法表示为．

14．某船在河中航行，已知顺流速度是14km/h,逆流速度是8km/h,那么它在静水中的速度是km/h,水流速度是km/h.

15．如图所示，在某一电路中，保持电压不变，电阻R（欧）与电流I（安）之间的函数关系式是．

三、解答题（本大题共9个题，满分63分）

18．如图所示，甲、乙两同学分别住在秀水大道两旁的A，B处，一天其中一人要到对方家中去复习功课，为了能最快速度到达，如何走最近？画图说明．

22．已知某商品的进价为每件40元．现在的售价是每件60元．每星期可卖出300件．市场调查反映：如调整价格，每涨价一元．每星期要少卖出10件；每降价一元，每星期可多卖出18件．如何定价才能使利润最大？

1．下列事件：
①在足球赛中，弱队战胜强队．
②抛掷1枚硬币，硬币落地时正面朝上．
③任取两个正整数，其和大于1
④长为3cm,5cm,9cm的三条线段能围成一个三角形．
其中确定事件有（　　）

2．如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（　　）

3．设a、b为x²+x-2011=0的两个实根，则a³+a²+3a+2014b=（　　）

5．如图，下列选项中不是正六棱柱三视图的是（　　）

6．如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合），OD⊥BC，OE⊥AC，垂足分别为D、E，在点C的运动过程中，下列说法正确的是（　　）

7．下列各组数中，相等的是（　　）

8．如图，在平面直角坐标系中，Q是直线y=-
1
2
x+2上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q'，连接OQ'，则OQ'的最小值为（　　）

9．计算：（-2a³）²的结果是（　　）

10．如图，小刀的刀柄DEFG是一个直角梯形（挖去一个半圆），刀片上下两边AD和BC平行，转动刀片到如图所示的位置，则∠ADE+∠BCE的度数为（　　）

11．有两组卡片，第一组卡片上分别写有数字“2，3，4”，第二组卡片上分别写有数字“3，4，5”，现从每组卡片中各随机抽出一张，用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字，差为负数的概率为

．

12．如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D，过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE，对于下列结论：①AD=DC；②△CBA∽△CDE；③
ˆ
BD
=
ˆ
AD
；④AE为⊙O的切线，一定正确的结论选项是

．

13．2019年4月10日，全球六地同步发布“事件视界望远镜”获取的首张“黑洞”照片，这个位于室女座足系团中的黑洞，质量约为太阳的6500000000倍．将6500000000用科学记数法表示为
．

14．某船在河中航行，已知顺流速度是14km/h,逆流速度是8km/h,那么它在静水中的速度是
km/h,水流速度是
km/h.

15．如图所示，在某一电路中，保持电压不变，电阻R（欧）与电流I（安）之间的函数关系式是
．