2022-2023学年河南省濮阳市清丰县仙庄中学八年级（下）期末数学试卷

一、选择题（每小题3分，共30分）

• 1．以下列各组数的长为边作三角形，不能构成直角三角形的是（　　）

  A．3，4，5

  B．4，5，6

  C．6，8，10

  D．9，12，15
  组卷：182引用：9难度：0.7

  解析

• 2．已知正比例函数y=kx,当x=2时，y=6，则下列各点在该函数图象上的是（　　）

  A．（-1，-3）

  B．（-1，3）

  C．（3，1）

  D．（-3，1）
  组卷：150引用：4难度：0.6

  解析

• 3．下列计算正确的是（　　）

  A． 4 =±2

  B． 2 + 3 = 5

  C． 8 ÷ 2 =2

  D． 8 =4
  组卷：87引用：3难度：0.8

  解析

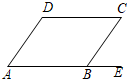• 4．如图，四边形ABCD是平行四边形，点E在线段AB的延长线上，若∠CBE=60°，则∠D的度数为（　　）

  A．100°

  B．110°

  C．120°

  D．130°
  组卷：79引用：3难度：0.6

  解析

• 5．为能很好地适应中考体育测试，某校九年级进行了3次体育模拟训练，甲、乙、丙三名同学成绩的平均分及方差S²如表所示，那么这三名同学模拟训练成绩最稳定的是（　　）
  

  	甲	乙	丙
  x	48	48	48
  S2	16	2	24

  A．甲

  B．乙

  C．丙

  D．无法确定
  组卷：69引用：3难度：0.8

  解析

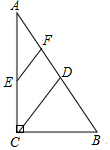• 6．如图，在Rt△ABC中，∠ACB=90°，∠A=30°，D，E，F分别为AB，AC，AD的中点，若BC=2，则EF的长度为（　　）

  A． 1 2

  B．1

  C． 3 2

  D． 3
  组卷：1633引用：17难度：0.7

  解析

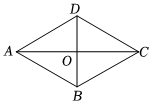• 7．如图，菱形ABCD的两条对角线相交于点O，若AC=6，BD=4，则菱形ABCD的周长是（　　）

  A．24

  B．16

  C．2 3

  D．4 13
  组卷：1518引用：16难度：0.9

  解析

三、解答题（共8题，共75分）

• 22．如图1，在矩形ABCD中，对角线AC、BD相交于点O，∠AOB=60°，AB=5cm,点P从点A出发沿AB以每秒1cm的速度向点B运动，同时点Q从点C出发沿CA方向以每秒2cm的速度向点A运动，设运动的时间为t秒，当点P运动到点B时，点Q停止运动．过点Q作QH⊥BC于点H．
  
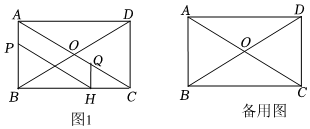
  （1）填空：∠ACB=

  °，HQ=

  ，AQ=

  （用含有t的式子表示）．
  （2）是否存在某一时刻t,使四边形APHQ为菱形？若存在，求出t的值：若不存在，请说明理由．
  （3）若在某一时刻t,平面内存在一点G，使P、Q、G、H四点构成的四边形是矩形，求出t的值．
  组卷：187引用：2难度：0.1

  解析

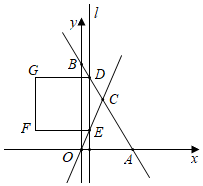• 23．如图，直线y=-2x+b分别与x轴、y轴交于A、B两点，与直线y=kx交于点C（2，4），平行于y轴的直线l从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，直线l分别交直线AB、直线OC于点D、E，以DE为边向左侧作正方形DEFG，当直线l经过点A时停止运动，设直线l的运动时间为t（秒）．
  求解以下问题：
  （1）b=

  ，k=

  ；
  （2）设线段DE的长度为d（d＞0），求d与t之间的函数关系式；
  （3）当正方形DEFG的边GF落在y轴上时，求出t的值．
  组卷：294引用：2难度：0.4

  解析