2023-2024学年湖北省鄂州市临空经济区三校联考八年级（上）月考数学试卷（10月份）
发布：2024/9/7 6:0:11
一、选择题（每小题3分，共30分）
-
1．如图，在△ABC中，作BC边上的高线，下列画法正确的是（ ）
组卷：473引用：14难度：0.5 -
2．具备下列条件的△ABC，不是直角三角形的是（ ）
组卷：4111引用：23难度：0.5 -
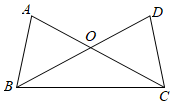3．如图，已知AB=DC，下列条件中，不能使△ABC≌△DCB的是（ ）组卷：2558引用：39难度：0.5 -
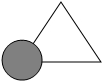4．如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）组卷：2622引用：75难度：0.7 -
5．如果一个正多边形的内角和等于720°，那么该正多边形的一个外角等于（ ）
组卷：1465引用：29难度：0.7 -
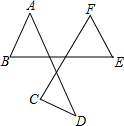6．如图，点A、B、C、D、E、F是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F的度数是（ ）组卷：5801引用：36难度：0.7 -
7．在△ABC中，AC=6，中线AD=10，则AB边的取值范围是（ ）
组卷：1234引用：8难度：0.6 -
8．一个多边形截去一个角后，形成的另一个多边形的内角和是1440°，则原来多边形的边数是（ ）
组卷：587引用：5难度：0.6
三、解答题（17题6分；18题6分；19题8分；20题8分；21题10分；22题10分；23题12分；24题12分）
-
23．【初步探索】
（1）如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；
【灵活运用】
（2）如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；
【拓展延伸】
（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．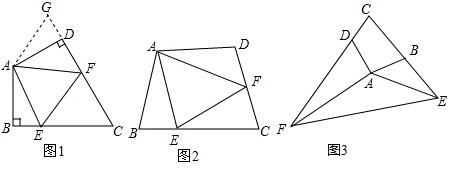
组卷：4608引用：52难度：0.1 -
24．如图，在平面直角坐标系中，点A（-6，0），点B在y轴正半轴上，AB=BC，∠CBA=90°．
（1）如图1，当B（0，1）时，连接AC交y轴于点D，写出点D的坐标；
（2）如图2，DB⊥y轴于B且BD=BO，连接CD交y轴于一点E，在B点运动的过程中，BE的长度是否会发生变化？若不变，求出BE的长度；若变化，请说明理由；
（3）如图3，N在AC延长线上，过N（t,-6）作NQ⊥x轴于Q，探究线段BN、AQ、BO之间的数量关系，并证明你的结论．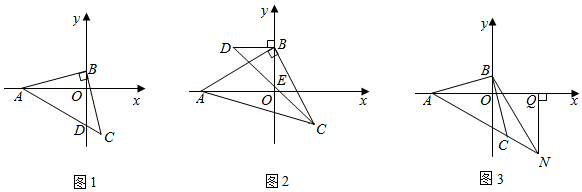
组卷：877引用：8难度：0.1
