2022-2023学年福建省厦门市思明区莲花中学八年级（下）期末数学试卷

一.选择题。（本大题有10小题，每小题4分，共40分.每小题都有四个选项，

• 1．若

  x

  +

  1

  有意义，则x的取值范围是（　　）

  A．x＞-1

  B．x≥0

  C．x≥-1

  D．任意实数
  组卷：762引用：12难度：0.9

  解析

• 2．下列各点在一次函数y=3x-2的图象上的是（　　）

  A．（2，3）

  B．（0，3）

  C．（-3，0）

  D．（3，7）
  组卷：447引用：3难度：0.6

  解析

• 3．下列说法中不正确的是（　　）

  A．两组对边分别平行的四边形是平行四边形

  B．对角线互相垂直的平行四边形是菱形

  C．有一个角是直角的平行四边形是矩形

  D．两条对角线互相垂直且相等的四边形是正方形
  组卷：360引用：3难度：0.7

  解析

• 4．关于x的方程x²-kx+9=0有两个相等的实数根，则k的值为（　　）

  A．9

  B．6

  C．±9

  D．±6
  组卷：419引用：9难度：0.7

  解析

• 5．某园林公司购进某种树苗，为了解该种树苗的移植成活率，现对购进的第一批树苗进行随机抽样并统计，结果如图所示．
  
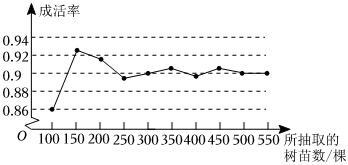
  若该公司第二批还需移植成活1800棵该种树苗，根据统计结果，则第二批树苗购买量较为合理的是（　　）

  A．1620棵

  B．1800棵

  C．2000棵

  D．2093棵
  组卷：557引用：5难度：0.7

  解析

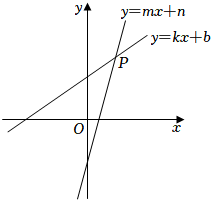• 6．如图，在平面直角坐标系xOy中，直线y=kx+b交直线y=mx+n于点P（1，2），则关于x的不等式kx+b＞mx+n的解集为（　　）

  A．x＞1

  B．x＞2

  C．x＜2

  D．x＜1
  组卷：382引用：5难度：0.6

  解析

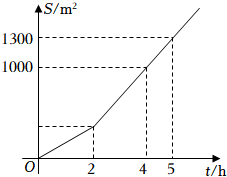• 7．某社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积S（单位：m²）与工作时间t（单位：h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（　　）

  A．150

  B．200m2

  C．250m2

  D．300m2
  组卷：399引用：4难度：0.7

  解析

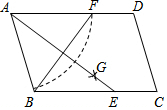• 8．如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，以A为圆心，AB长为半径画弧交AD于F，若BF=AB=10，则AE的长为（　　）

  A．10

  B． 10 5

  C． 10 3

  D． 5 3
  组卷：267引用：5难度：0.5

  解析

三、解答题。（共9小题，共86分）

• 24．已知，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2．
  ​
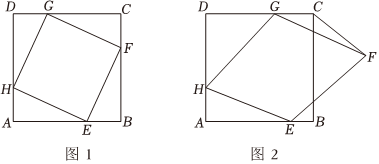
  （1）如图1，当DG=2，且点F在边BC上时，求证：
  ①△AHE≌△DGH；
  ②菱形EFGH是正方形．
  （2）如图2，当点F在正方形ABCD的外部时，连接CF．探究：点F到直线CD的距离是否发生变化？并说明理由．
  组卷：152引用：1难度：0.4

  解析

• 25．在平面直角坐标系xOy中，点M（-1，m），N（-1，n），原点O关于直线MN的对称点为A，直线OM，AN交于点P．
  （1）填空：①点A的坐标是

  ；②当m=1，n=-2时，点P的坐标为

  ；
  （2）连接ON，若n=-2m,△ONP的面积为12，求m的值；
  （3）过点P作MN的垂线，垂足为Q，连接OQ，若mn=-1（m≠±1），求证：PQ=OQ．
  组卷：282引用：5难度：0.1

  解析