2022-2023学年山东省青岛市崂山区八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．若分式

  1

  x

  -

  3

  有意义，则x满足的条件是（　　）

  A．x=3

  B．x＜3

  C．x＞3

  D．x≠3
  组卷：246引用：11难度：0.9

  解析

• 2．已知a＜b,下列不等式中，变形正确的是（　　）

  A．a-3＞b-3

  B． a 3 ＞ b 3

  C．3a-1＞3b-1

  D．-3a＞-3b
  组卷：194引用：2难度：0.9

  解析

• 3．以下分别是回收、节水、绿色包装、低碳4个标志，其中是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：136引用：6难度：0.9

  解析

• 4．下列命题中，其逆命题为真命题的是（　　）

  A．内错角相等	B．若a=b,则a2=b2
  C．对顶角相等	D．等腰三角形两底角相等
  组卷：64引用：1难度：0.7

  解析

• 5．下列等式从左到右变形中，属于因式分解的是（　　）

  A．a（x+y）=ax+ay	B．x2-2x+1=x（x-2）+1
  C．（x+1）（x-1）=x2-1	D．x2-1=（x+1）（x-1）
  组卷：1113引用：6难度：0.9

  解析

• 6．不等式组

  x + 2 ＞ 0

  2 x - 3 ≤ 1

  的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：345引用：14难度：0.9

  解析

• 7．用反证法证明命题“已知在△ABC中，AB=AC，则∠B＜90°”时，首先应该假设（　　）

  A．∠B≥90°	B．∠B＞90°
  C．AB≠AC	D．AB≠AC且∠B≥90°
  组卷：1033引用：16难度：0.7

  解析

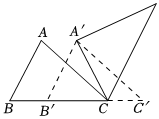• 8．如图，△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕A′逆时针旋转一定角度，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为（　　）

  A．4，30°

  B．2，60°

  C．1，60°

  D．3，30°
  组卷：262引用：1难度：0.5

  解析

四、解答题（本题满分共62分）

• 25．图形定义：四边形ABCD若满足∠A+∠C=180°，则我们称该四边形为“对角互补四边形”．
  （1）若四边形ABCD为对角互补四边形，且∠B：∠C：∠D=2：3：4，则∠A的度数为

  ．
  （2）如图1，四边形ABCD为对角互补四边形，∠BAD=∠BCD=90°，AB=AD．
  求证：AC平分∠BCD．
  小云同学是这么做的：延长CD至M，使得DM=BC，连AM，可证明△ABC≌△ADM，得到△ACM是等腰直角三角形，由此证明出AC平分∠BCD，还可以知道CB，CD，CA三者关系为：

  ；
  （3）如图2，四边形ABCD为对角互补四边形，且满足∠ABC=60°，AD=CD，则BA，BC，BD三者关系为：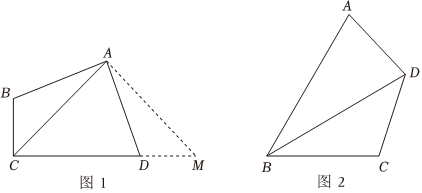

  ．
  
  组卷：318引用：1难度：0.2

  解析

• 26．如图，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A，B分别在x轴与y轴上，已知OA=6，OB=10．点D为y轴上一点，其坐标为（0，2），点P从点A出发以每秒2个单位的速度沿线段AC-CB的方向运动，当点P与点B重合时停止运动，运动时间为t秒．
  （1）当点P经过点C时，求直线DP的函数解析式；
  （2）求△OPD的面积S关于t的函数解析式；
  （3）点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．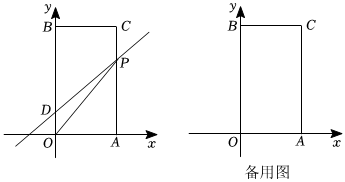
  
  组卷：612引用：3难度：0.3

  解析