2023-2024学年天津市和平区八年级（上）期中数学试卷
发布：2024/10/2 17:0:2
一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只
-
1．下面的图案中，不是轴对称图形的是（ ）
组卷：27引用：1难度：0.8 -
2．等腰三角形的周长为18cm,其中一边长为4cm,则该等腰三角形的腰长为（ ）
组卷：109引用：2难度：0.7 -
3．若正多边形的一个外角为30°，则该正多边形为（ ）
组卷：959引用：10难度：0.5 -
4．在平面直角坐标系中，点A（2，3）关于x轴对称的点的坐标是（ ）
组卷：597引用：16难度：0.8 -
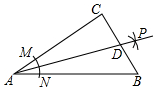5．如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交边AC、AB于点M、N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（ ）组卷：231引用：5难度：0.6 -
6．如图，已知MB=ND，∠MBA=∠NDC，不能判定△ABM≌△CDN的是（ ）组卷：420引用：4难度：0.7 -
7．如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=3cm,则AB的长为（ ）组卷：96引用：3难度：0.7 -
8．如图，∠BCD是△ABC的外角，∠A=40°，∠B=70°，则∠BCD的度数为（ ）组卷：162引用：5难度：0.7
三、解答题（本大题共7小题，共46分.解答应写出文字说明、演算步骤或推理过程）
-
24．在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE=度；
（2）设∠BAC=α，∠DCE=β．
①如图2，当点D在线段CB上，∠BAC≠90°时，请你探究α与β之间的数量关系，并证明你的结论；
②如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时α与β之间的数量关系（不需证明）．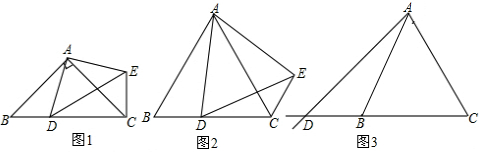
组卷：5362引用：45难度：0.5 -
25．数学课上，李老师出示了如下的题目：
“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图，试确定线段AE与DB的大小关系，并说明理由”．
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE DB（填“＞”，“＜”或“=”）．
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE DB（填“＞”，“＜”或“=”）．理由如下：如图2，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）．
组卷：11962引用：39难度：0.3
