2023年吉林省长春市九台区中考数学二模试卷

一、单选题（每小题3分，共24分）、

• 1．在实数-

  2

  ，

  1

  2

  ，0，-2中，最大的数是（　　）

  A．- 2

  B． 1 2

  C．0

  D．-2
  组卷：62引用：4难度：0.7

  解析

• 2．第24届冬奥会于2022年2月4日至2月20日在中国北京和张家口成功举办，本届冬奥会的运动员达到2892人，历史规模第二．数据2892用科学记数法表示应是（　　）

  A．0.2892×104

  B．2.892×104

  C．2.892×103

  D．28.92×103
  组卷：49引用：2难度：0.9

  解析

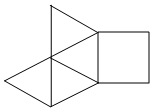• 3．某几何体的表面展开图如图所示，这个几何体是（　　）

  A．圆柱

  B．长方体

  C．四棱锥

  D．五棱锥
  组卷：461引用：4难度：0.8

  解析

• 4．不等式3x-1≥5x+1的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：141引用：3难度：0.6

  解析

• 5．如图，电线杆AB的中点C处有一标志物，在地面D点处测得标志物的仰角为32°，若点D到电线杆底部点B的距离为a米，则电线杆AB的长可表示为（　　）

  A． a sin 32 °	B． 2 a tan 32 ° 米
  C．2a ⋅ tan 32 ° 米	D．2a ⋅ cos 32 ° 米
  组卷：136引用：3难度：0.5

  解析

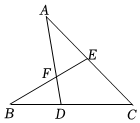• 6．如图，点D、E分别在线段BC、AC上，连接AD、BE．若∠A=35°，∠B=30°，∠C=45°，则∠AFB的大小为（　　）

  A．75°

  B．80°

  C．100°

  D．110°
  组卷：650引用：3难度：0.7

  解析

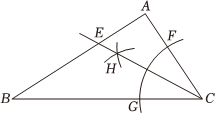• 7．如图，在Rt△ABC中，∠BAC=90°，按下列方式作图：①以点C为圆心，适当长为半径画弧，分别交AC，BC于点F，G；②分别以点F，G为圆心，大于CF的长度为半径画弧，两弧交于点H；③作射线CH交AB于点E，若AE=2，BC=7．则△BEC的面积为（　　）

  A．7

  B．8

  C．14

  D．16
  组卷：53引用：1难度：0.5

  解析

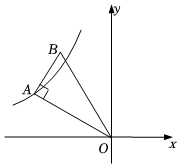• 8．在如图，Rt△AOB中，∠BAO=90°，∠B=60°，△AOB的面积为6，AO与x轴负半轴的夹角为30°，双曲线y=

  k

  x

  经过点A，则k的值为（　　）

  A． - 9 2

  B．-9

  C． - 2 3

  D．-6
  组卷：1662引用：8难度：0.5

  解析

三、解答题（本大题共10小题，共78分）

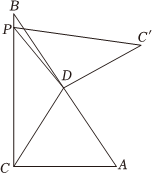• 23．如图，在Rt△ABC中，∠ACB=90°，AC=1，

  BC

  =

  2

  ，点D为AB的中点，动点P在BC上（点P与点C不重合），做点C关于直线PD的对称点C′，连结PD、C′D．
  （1）线段AB的长为

  ．
  （2）设C'到AC的距离为h,求h的最大值．
  （3）当△PDC'是锐角三角形时，求PC的取值范围．
  （4）当直线PC'与△ABC的一条边平行时，直接写出PC的长．
  组卷：124引用：1难度：0.5

  解析

• 24．在平面直角坐标系中，抛物线y=-x²+bx+c（b、c为常数）的对称轴为直线x=1，与y轴交点坐标为（0，3）．
  （1）求此抛物线对应的函数表达式．
  （2）当点（m-1，1）在此抛物线上，且抛物线在x＞m时，y随x的增大而减小，求m的值．
  （3）点A、点B均在这个抛物线上（点A在点B的左侧），点A的横坐标为m,点B的横坐标为4-m.
  将此抛物线上A、B两点之间的部分（包括A、B两点）记为图象G
  ①当点A在x轴上方，图象的最高点到两坐标轴的距离和为p,图象的最低点到x轴的距离为q,当q=

  1

  2

  p时，求m的值．​
  ②设点D（m,m），点E（m,1-m），将线段DE绕点D逆时针旋转90°后得到线段DF，连结EF，当△DEF和图象G有公共点时，直接写出m的取值范围．
  组卷：209引用：1难度：0.2

  解析