2022-2023学年四川省成都七中高新校区九年级（上）期中数学试卷

一、选择题（本大题共8个小题，每个小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）

• 1．若m²=4，则m=（　　）

  A．2

  B．-2

  C．±2

  D．± 2
  组卷：293引用：2难度：0.9

  解析

• 2．将一元二次方程（x-2）（x+3）=12化为一般形式ax²+bx+c=0（a≠0，a,b,c为常数），其中c的值是（　　）

  A．-18

  B．-6

  C．6

  D．18
  组卷：413引用：5难度：0.8

  解析

• 3．关于x的一元二次方程x²-2x+a=0有两个相等的实数根，则a的值是（　　）

  A．4

  B．-4

  C．1

  D．-1
  组卷：1256引用：13难度：0.9

  解析

• 4．在▱ABCD中，若∠A：∠B=1：2，则∠A的度数是（　　）

  A．60°

  B．90°

  C．120°

  D．150°
  组卷：301引用：9难度：0.9

  解析

• 5．一个不透明的盒子中装有5个大小相同的乒乓球，将其摇匀，从中随机摸出一个乒乓球，记下其颜色．然后再放回，这样重复做了1000次摸球试验，摸到黄球的频数为399，则估计其中的黄球个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：195引用：3难度：0.7

  解析

• 6．已知△ABC∽△DEF，且∠A=30°，∠E=60°，则∠C的度数是（　　）

  A．30°

  B．60°

  C．90°

  D．120°
  组卷：175引用：3难度：0.6

  解析

• 7．如图，l₁∥l₂，直线AB分别交l₁，l₂于A，B两点，直线CD分别交l₁，l₂，AB于点C，D，E，则下列说法一定正确的是（　　）

  A． AC BD = CD AB

  B． AC BD = AE AB

  C． AC BD = AE BE

  D． AC BD = BE AB
  组卷：215引用：2难度：0.6

  解析

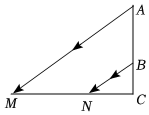• 8．如图，AB表示一个窗户的高，AM和BN表示，射入室内的光线，窗户的下端到地面距离BC=1米，已知某一时刻BC在地面的影长CN=1.5米，AC在地面的影长CM=4.5米，则AB高为（　　）米．

  A．3.5

  B．2

  C．1.5

  D．2.5
  组卷：477引用：10难度：0.7

  解析

二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）

• 25．如图，在平面直角坐标系xOy中，一次函数y=ax+b的图象l₁分别与x,y轴交于A（10，0），B（0，5）两点，过点O的直线l₂与线段AB交于点C．
  （1）求直线l₁的表达式；
  （2）若AO²=AB•AC，求直线l₂的表达式：
  （3）在（2）的条件下，当x＜m时，对于x的每一个值，不等式组2x＜kx+1＜-

  1

  2

  x+5均成立，直接写出k的取值范围．
  组卷：294引用：2难度：0.2

  解析

• 26．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
  （1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
  （2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．
  （3）如图2，△ABC中，AC=2，BC=

  2

  ，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．
  
  组卷：7944引用：40难度：0.3

  解析