2022-2023学年湖北省黄冈市武穴市八年级（下）期末数学试卷

一、选择题（共8小题，每小题3分，共24分）

• 1．下列运算正确的是（　　）

  A． 2 + 3 = 5

  B． 2 2 × 3 2 = 6 2

  C． 8 ÷ 2 = 2

  D． 3 2 - 2 = 3
  组卷：3017引用：81难度：0.9

  解析

• 2．下列各组数据中的三个数，可作为三边长构成直角三角形的是（　　）

  A．4，5，6

  B．2，3，4

  C．11，12，13

  D．8，15，17
  组卷：243引用：8难度：0.9

  解析

• 3．下列式子为最简二次根式的是（　　）

  A． 5

  B． 12

  C． a 2

  D． 1 a
  组卷：3029引用：26难度：0.9

  解析

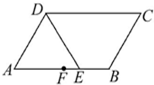• 4．如图，在平行四边形ABCD中，DE是∠ADC的平分线，F是AB的中点，AB=6，AD=4，则AE：EF：BE为（　　）

  A．4：1：2

  B．4：1：3

  C．3：1：2

  D．5：1：2
  组卷：1251引用：42难度：0.5

  解析

• 5．某校评选先进班集体，从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分，各项满分均为100，所占比例如下表：
  

  项目	学习	卫生	纪律	活动参与
  所占比例	40%	25%	25%	10%

  八年级2班这四项得分依次为80，90，84，70，则该班四项综合得分（满分100）为（　　）

  A．81.5

  B．82.5

  C．84

  D．86
  组卷：1296引用：25难度：0.6

  解析

• 6．已知一次函数y=kx+k,若y随x的减小而减小，则该函数的图象经过（　　）

  A．第一、二、三象限	B．第一、二、四象限
  C．第一、三、四象限	D．第二、三、四象限
  组卷：241引用：1难度：0.9

  解析

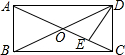• 7．如图，矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3：2，则∠BDE的度数为（　　）

  A．36°

  B．9°

  C．27°

  D．18°
  组卷：1633引用：20难度：0.7

  解析

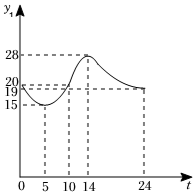• 8．遵义市某天的气温y₁（单位：℃）随时间t（单位：h）的变化如图所示，设y₂表示0时到t时气温的值的极差（即0时到t时范围气温的最大值与最小值的差），则y₂与t的函数图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：788引用：7难度：0.6

  解析

三、解答题（共8小题，共计72分）

• 23．在Rt△ABC与Rt△BDE中，∠ABC=∠DBE=90°，AB=BC，BD=BE．
  （1）如图1，若点D，B，C在同一直线上，连接AD，CE，则AD与CE的关系为

  ；
  （2）如果将图1中的△BDE绕点B在平面内顺时针旋转到如图2的位置，那么请你判断AD与CE的关系，并说明理由；
  （3）如图3，若AB=6，BD=2，连接AE，分别取DE，AE，AC的中点M，P，N，连接MP，NP，MN，将△BDE绕点B在平面内顺时针旋转一周，请直接写出旋转过程中△MPN面积的最小值和最大值．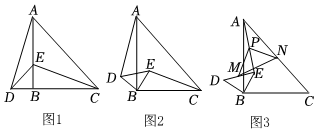
  
  组卷：287引用：4难度：0.4

  解析

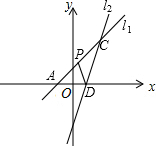• 24．如图，在平面直角坐标系xOy中，直线l₁：y=x+2与x轴交于点A，直线l₂：y=3x-6与x轴交于点D，与l₁相交于点C．
  （1）求点D的坐标；
  （2）在y轴上一点E，若S_△ACE=S_△ACD，求点E的坐标；
  （3）直线l₁上一点P（1，3），平面内一点F，若以A、P、F为顶点的三角形与△APD全等，求点F的坐标．
  组卷：2682引用：5难度：0.2

  解析