2023年黑龙江省绥化市中考数学适应性试卷

一、单项选择题（每小题3分，共36分）

• 1．一个有理数的倒数是它本身，这个数是（　　）

  A．0

  B．1

  C．-1

  D．1或-1
  组卷：959引用：20难度：0.9

  解析

• 2．下列图形中，不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：10引用：1难度：0.9

  解析

• 3．下列运算正确的是（　　）

  A．2 1 2 =1	B． 2 3 × 3 3 = 6 3
  C．（-a）3•a2=-a5	D．（2a2）3=6a6
  组卷：74引用：2难度：0.8

  解析

• 4．下面四个图形中，是三棱柱的平面展开图的是（　　）

  A．

  B．

  C．

  D．
  组卷：642引用：83难度：0.9

  解析

• 5．下列函数中，自变量x的取值范围是x＞2的函数是（　　）

  A． y = x - 2

  B． y = 2 x - 1

  C． y = 1 x - 2

  D． y = 1 2 x - 1
  组卷：434引用：92难度：0.9

  解析

• 6．下列命题是真命题的是（　　）

  A．相等的角是对顶角

  B．两直线与第三条直线相交，同位角相等

  C．任意多边形的外角和为360°

  D．对角线相等的四边形是矩形
  组卷：10引用：1难度：0.5

  解析

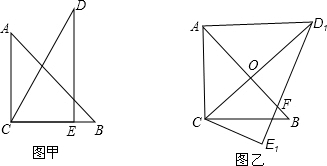• 7．把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D₁CE₁（如图乙），此时AB与CD₁交于点O，则线段AD₁的长为（　　）

  A． 3 2

  B．5

  C．4

  D． 31
  组卷：4563引用：94难度：0.5

  解析

• 8．16位参加百米半决赛同学的成绩各不相同，按成绩取前8位进入决赛．如果小刘知道了自己的成绩后，要判断能否进入决赛，其他15位同学成绩的下列数据中，能使他得出结论的是（　　）

  A．平均数

  B．极差

  C．中位数

  D．方差
  组卷：157引用：26难度：0.9

  解析

• 9．甲、乙两人同时分别从A，B两地沿同一条公路骑自行车到C地．已知A，C两地间的距离为110千米，B，C两地间的距离为100千米．甲骑自行车的平均速度比乙快2千米/时．结果两人同时到达C地．求两人的平均速度，为解决此问题，设乙骑自行车的平均速度为x千米/时．由题意列出方程．其中正确的是（　　）

  A． 110 x + 2 = 100 x	B． 110 x = 100 x + 2
  C． 110 x - 2 = 100 x	D． 110 x = 100 x - 2
  组卷：3000引用：80难度：0.9

  解析

三、简答题（共54分）

• 27．如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．
  （1）试说明CE是⊙O的切线；
  （2）若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB；
  （3）设点D是线段AC上任意一点（不含端点），连接OD，当

  1

  2

  CD+OD的最小值为6时，求⊙O的直径AB的长．
  组卷：4461引用：9难度：0.1

  解析

• 28．​​如图，在平面直角坐标系中，O为坐标原点，抛物线y=

  1

  2

  x²+2x与x轴相交于点O，B，顶点，连接OA．
  （1）点A的坐标和∠AOB的度数；
  （2）将抛物线

  y

  =

  1

  2

  x

  2

  +

  2

  x

  向右平移4个单位长度，再向下平移2个单位长度，得到抛物线其顶点为C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′，试判断其形状，说明理由；
  （3）（2）的情况下，判断点C′是否在抛物线

  y

  =

  1

  2

  x

  2

  +

  2

  x

  上，请说明理由；
  （4）P为x轴上的一个动点，在抛物线M上是否存在点Q，使以O，P，C，Q为顶点的四边形平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
  组卷：159引用：1难度：0.1

  解析