当前位置：试卷中心 > 试卷详情

2023年贵州省遵义五十七中中考数学四模试卷

发布：2024/5/11 8:0:9

一、选择题（本题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满．）

1．5的倒数是（　　）
A．5 B．-5 C．
1
5
D．
-
1
5
组卷：190引用：10难度：0.8
解析
2．计算（-a²）³正确的结果是（　　）
A．a⁶ B．a⁵ C．-a⁵ D．-a⁶
组卷：81引用：1难度：0.7
解析
3．在一个不透明的盒子中，装有质地、大小完全相同的白色乒乓球2个，黄色乒乓球3个．随机摸出1个球，摸到黄色乒乓球的概率是（　　）
A．
2
3
B．
3
5
C．
1
5
D．
2
5
组卷：36引用：2难度：0.6
解析
4．计算
2
a
a
+
2
+
2
-
a
a
+
2
的结果为（　　）
A．1 B．-1 C．
a
+
2
（
a
+
2
）
2
D．
a
+
2
2
-
a
组卷：73引用：3难度：0.8
解析
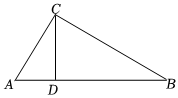5．如图，在△ABC中，D是AB边上的点，∠B=∠ACD，AC：AB=1：2，则△ACD与△ABC的面积比是（　　）
A．1：
2
B．1：2 C．1：3 D．1：4
组卷：138引用：2难度：0.7
解析
6．圆锥的底面半径是5cm,侧面展开图的圆心角是180°，圆锥的高是（　　）
A．5
3
cm B．10cm C．6cm D．5cm
组卷：2247引用：11难度：0.8
解析
7．新能源汽车节能、环保，越来越受消费者喜爱，各种品牌相继投放市场，我国新能源汽车近几年销量全球第一，2016年销量为50.7万辆，销量逐年增加，到2018年销量为125.6万辆．设年平均增长率为x,可列方程为（　　）
A．50.7（1+x）²=125.6 B．125.6（1-x）²=50.7
C．50.7（1+2x）=125.6 D．50.7（1+x²）=125.6
组卷：1796引用：21难度：0.6
解析
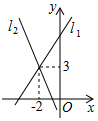8．如图所示，直线l₁：y=
3
2
x+6与直线l₂：y=-
5
2
x-2交于点P（-2，3），不等式
3
2
x+6＞-
5
2
x-2的解集是（　　）
A．x＞-2 B．x≥-2 C．x＜-2 D．x≤-2
组卷：3693引用：26难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三．解答题（本题共9小题，共98分，解答时应写出必要的文字说明、证明过程或演算步骤）．

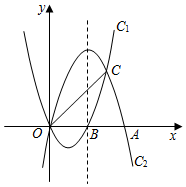24．如图，抛物线C₁：y=x²-2x与抛物线C₂：y=ax²+bx开口大小相同、方向相反，它们相交于O，C两点，且分别与x轴的正半轴交于点B，点A，OA=2OB．
（1）求抛物线C₂的解析式；
（2）在抛物线C₂的对称轴上是否存在点P，使PA+PC的值最小？若存在，求出点P的坐标，若不存在，说明理由；
（3）M是直线OC上方抛物线C₂上的一个动点，连接MO，MC，M运动到什么位置时，△MOC面积最大？并求出最大面积．
组卷：5064引用：12难度：0.4
解析
25．如图1，在矩形ABCD中，AB=10，AD=8，E是AD边上的一点，连接CE，将矩形ABCD沿CE折叠，顶点D恰好落在AB边上的点F处，延长CE交BA的延长线于点G．

（1）求线段AE的长；
（2）求证四边形DGFC为菱形；
（3）如图2，M，N分别是线段CG，DG上的动点（与端点不重合），且∠DMN=∠DCM，设DN=x,是否存在这样的点N，使△DMN是直角三角形？若存在，请求出x的值；若不存在，请说明理由．
组卷：1429引用：8难度：0.1
解析