2022-2023学年河南省安阳市文峰区飞翔中学八年级(上)期中数学试卷
发布:2024/9/27 12:0:2
一.选择题(共10小题)
-
1.下列四个图形中是轴对称图形的是( )
组卷:10引用:3难度:0.8 -
2.下列长度的三条线段,能组成三角形的是( )
组卷:176引用:5难度:0.8 -
3.△ABC中BC边上的高作法正确的是( )
组卷:1290引用:25难度:0.9 -
4.下列运算正确的是( )
组卷:1002引用:5难度:0.8 -
5.在平面直角坐标系中,点A(1,-2)关于x轴对称的点的坐标是( )
组卷:590引用:13难度:0.9 -
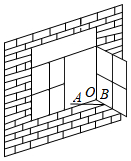 6.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )组卷:266引用:17难度:0.8
6.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )组卷:266引用:17难度:0.8 -
7.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
组卷:4645引用:72难度:0.9
三.解答题(共8小题)
-
22.人教版八年级数学上册教材中这样写道:“我们把多项式a2+2ab+b2及a2-2ab+b2这样的式子叫做完全平方式”.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值、最小值等.
例如:分解因式x2+2x-3.
原式=(x2+2x+1-1)-3=(x+1)2-4=(x+1+2)(x+1-2)=(x+3)(x-1).
求代数式2x2+4x-6的最小值.
2x2+4x-6=2(x2+2x+1-1)-6=2(x+1)2-8,可知当x=-1时,2x2+4x-6有最小值-8.
根据阅读材料用配方法解决下列问题:
(1)填空:x2-6x+=(x-3)2;2m2+4m=2(m+1)2-;
(2)利用配方法分解因式:x2+4x-12;
(3)当x为何值时,多项式-2x2-4x+8有最大值?并求出这个最大值.组卷:689引用:2难度:0.7 -
23.【阅读材料】小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
【材料理解】(1)在图1中证明小明的发现.
【深入探究】(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°,其中正确的有 .(将所有正确的序号填在横线上)
【延伸应用】(3)如图3,在四边形ABCD中,BD=CD,AB=BE,∠ABE=∠BDC=60°,试探究∠A与∠BED的数关系,并证明.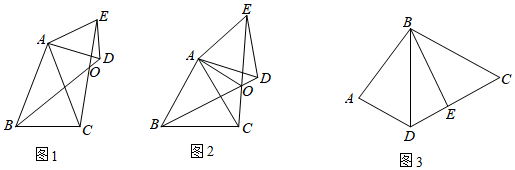 组卷:859引用:8难度:0.4
组卷:859引用:8难度:0.4


