2023-2024学年江苏省苏州市工业园区星湾学校、星汇学校八年级（上）调研数学试卷（10月份）
发布：2024/9/15 1:0:9
一．选择题（本题共10小题，每题2分，共20分）
-
1．在下列四个亚运会图标中，属于轴对称图形的是（ ）
组卷：38引用：2难度：0.9 -
2．下列各组数中，是勾股数的是（ ）
组卷：108引用：2难度：0.5 -
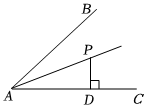3．如图，AP平分∠BAC，PD⊥BC于点D，若PD=4，则P到AB的距离是（ ）组卷：122引用：5难度：0.5 -
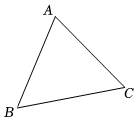4．如图，某市的三个城镇中心A、B、C构成△ABC，该市政府打算修建一个大型体育中心P，使得该体育中心到三个城镇中心A、B、C的距离相等，则P点应设计在（ ）组卷：1738引用：11难度：0.7 -
5．等腰三角形的两边长为3cm,6cm,则该三角形的周长为（ ）
组卷：167引用：4难度：0.9 -
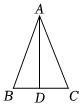6．如图，△ABC中，AB=AC，AD⊥BC于点D，则下列结论不一定成立的是（ ）组卷：226引用：3难度：0.9 -
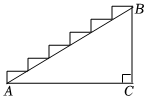7．如图所示的一段楼梯，高BC是3米，斜边AB长是5米，现打算在楼梯上铺地毯，至少需要地毯的长度为（ ）组卷：1117引用：8难度：0.5 -
8．如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是（ ）
组卷：1051引用：103难度：0.5 -
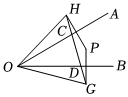9．如图，点P是∠AOB内部一点，点P关于OA、OB的对称点是H、G，直线HG交OA、OB于点C、D，若HG=4cm,且∠AOB=30°，则△HOG的周长是（ ）组卷：370引用：2难度：0.5
三．解答题（共9小题）
-
26．角平分线的轴对称性可以为解题提供思路和方法：
（1）如图1，在∠MON的两边上取两点A、B，使OA=OB，点P为角平分线上任意一点，连接PA、PB，根据角的轴对称性易得 ；
（2）如图2，△ABC中，AB＞AC，求证：∠C＞∠B．
证明：作∠BAC的平分线交BC边于点D，在AB边上截取AE=AC，连接ED．（请完成证明）
（3）如图3，在△ABC中，∠B=2∠C，AD为∠BAC的角平分线，写出AB、BD、AC之间的数量关系并说明理由．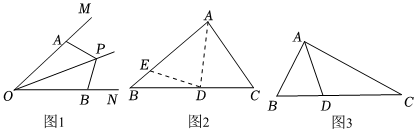
组卷：83引用：1难度：0.5 -
27．如图1所示，在△ABC中，AB=AC，∠BAC=α（α＞90°），D为BC边上的一个动点，将△ABD沿AD折叠，得到△AED，且点E在直线BC的下方．
（1）如图2，当AE⊥BC时，垂足为H，
①若α=100°，则∠BAD的度数为 ；
②若AB=10，BC=16，求BD的长；
（2）若再次折叠图1中的△ABC，使AC与AE重合，得到折痕AF（点F在CD上），连接EF，若△DEF是等腰三角形，则∠BAD=（用含α的代数式表示）．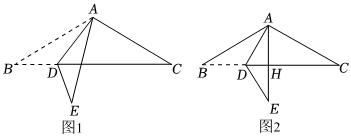
组卷：141引用：1难度：0.5
