2022-2023学年天津市津南区咸水沽二中九年级（上）期中数学试卷

一．选择题（本大题共12小题，每小题3分，共36分）

• 1．下列事件是必然事件的是（　　）

  A．掷一次骰子，向上一面点数大于0

  B．打开电视新闻频道正在播报体育新闻

  C．经过有交通信号灯的路口，遇到红灯

  D．任意画一个三角形其内角和是360°
  组卷：156引用：5难度：0.7

  解析

• 2．下列方程中，是一元二次方程的是（　　）

  A．4（x+2）=25

  B．2x2+3x-1=0

  C．x+y=0

  D． 1 x + 2 =4
  组卷：212引用：4难度：0.9

  解析

• 3．用配方法解方程x²+8x+3=0，正确的变形为（　　）

  A．（x-4）2=13

  B．（x+4）2=5

  C．（x+4）2=13

  D．（x+4）2=-5
  组卷：322引用：6难度：0.6

  解析

• 4．一元二次方程x²-7x-2=0的实数根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．没有实数根	D．不能确定
  组卷：889引用：20难度：0.9

  解析

• 5．一元二次方程x²-5x+6=0的解为（　　）

  A．x1=2，x2=-3	B．x1=-2，x2=3
  C．x1=-2，x2=-3	D．x1=2，x2=3
  组卷：2459引用：29难度：0.8

  解析

• 6．将二次函数y=6x²的图象先向右平移2个单位长度，再向下平移3个单位长度，得到的函数图象的解析式是
  （　　）

  A．y=6（x+2）2+3	B．y=6（x-2）2+3
  C．y=6（x+2）2-3	D．y=6（x-2）2-3
  组卷：107引用：9难度：0.9

  解析

• 7．关于抛物线y=-（x+1）²+2，下列说法错误的是（　　）

  A．图象的开口向下

  B．当x＞-1时，y随x的增大而减少

  C．图象的顶点坐标是（-1，2）

  D．图象与y轴的交点坐标为（0，2）
  组卷：992引用：2难度：0.7

  解析

• 8．若A（-2，y₁），B（-1，y₂），C（2，y₃）为二次函数y=x²+2x+2的图象上的三点，则y₁，y₂，y₃的大小关系是（　　）

  A．y1＜y2＜y3

  B．y1＜y3＜y2

  C．y2＜y1＜y3

  D．y3＜y1＜y2
  组卷：883引用：22难度：0.6

  解析

四．解答题（本大题共5小题，共56分）

• 23．某水果店销售某品牌苹果，该苹果每箱的进价是40元，若每箱售价60元，每星期可卖180箱．为了促销，该水果店决定降价销售．市场调查反映：若售价每降价1元，每星期可多卖10箱．设该苹果每箱售价x元（40≤x≤60），每星期的销售量为y箱．
  （1）求y与x之间的函数关系式；
  （2）当每箱售价为多少元时，每星期的销售利润最大，最大利润多少元？
  组卷：184引用：3难度：0.5

  解析

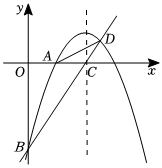• 24．如图，已知抛物线y=ax²+4x+c经过A（2，0）、B（0，-6）两点，其对称轴与x轴交于点C．
  （1）求该抛物线和直线BC的解析式；
  （2）设抛物线与直线BC相交于点D，求△ABD的面积；
  （3）在该抛物线的对称轴上是否存在点Q，使得△QAB的周长最小？若存在，求出Q点的坐标及△QAB最小周长；若不存在，请说明理由．
  组卷：517引用：11难度：0.3

  解析