2023-2024学年山东省日照市东港区新营中学九年级（上）月考数学试卷（10月份）

一.选择题（每题3分，共36分）

• 1．中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”，其中既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：2608引用：78难度：0.9

  解析

• 2．如果关于x的方程ax²+bx+c=0（a≠0）中a-b+c=0，那么方程必有一个根是（　　）

  A．1

  B．-1

  C．0

  D．2
  组卷：294引用：12难度：0.9

  解析

• 3．用配方法解一元二次方程x²+4x+1=0，下列变形正确的是（　　）

  A．（x-2）2-3=0	B．（x+4）2-15=0
  C．（x+2）2=3	D．（x-4）2=15
  组卷：46引用：7难度：0.7

  解析

• 4．在同一平面直角坐标系xOy中，一次函数y=ax与二次函数y=ax²+a的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：2628引用：16难度：0.6

  解析

• 5．定义运算：m☆n=n²-mn-1，例如：3☆2=2²-3×2-1=-3．则方程2☆x=0的根的情况为（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．无实数根	D．只有一个实数根
  组卷：494引用：7难度：0.5

  解析

• 6．把抛物线y=3（x-2）²+1向下平移3个单位长度，再向左平移4个单位长度，得到的抛物线解析式为（　　）

  A．y=3（x+1）2+5	B．y=3（x+2）2-2
  C．y=3（x-6）2-2	D．y=3（x+2）2+4
  组卷：128引用：3难度：0.7

  解析

• 7．若a,b是方程x²+2x-2024=0的两个实数根，则a²+3a+b的值是（　　）

  A．2021

  B．2022

  C．2023

  D．2024
  组卷：634引用：13难度：0.7

  解析

三.解答题（6道大题，共72分）

• 21．阅读下面材料，并解决问题：
  （1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
  为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB=

  ；
  （2）基本运用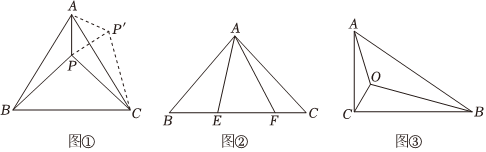
  
  请你利用第（1）题的解答思想方法，解答下面问题
  已知如图②，△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点且∠EAF=45°，求证：EF²=BE²+FC²；
  （3）能力提升
  如图③，在Rt△ABC中，∠ACB=90°，AC=1，∠ABC=30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC=∠COB=∠BOA=120°，求OA+OB+OC的值．
  组卷：12927引用：44难度：0.5

  解析

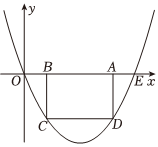• 22．如图，抛物线过点O（0，0），E（10，0），矩形ABCD的边AB在线段OE上（点B在点A的左侧），点C，D在抛物线上．设B（t,0），当t=2时，BC=4．
  （1）求抛物线的函数表达式；
  （2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？
  （3）保持t=2时的矩形ABCD不动，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，求抛物线平移的距离．
  组卷：3624引用：16难度：0.2

  解析