2023-2024学年北京市朝阳区陈经纶中学九年级（上）月考数学试卷（10月份）

一、选择题

• 1．在我国古代的房屋建筑中，窗棂是重要的组成部分，具有高度的艺术价值．下列窗棂的图案中，是中心对称图形但不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：174引用：8难度：0.9

  解析

• 2．方程x²-x+3=0的根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．无实数根	D．只有一个实数根
  组卷：1136引用：21难度：0.8

  解析

• 3．如果点M（-2，y₁），N（-1，y₂）在二次函数y=-x²+2x的图象上，那么下列结论正确的是（　　）

  A．y1≤y2

  B．y1＞y2

  C．y1＜y2

  D．y1≥y2
  组卷：8引用：2难度：0.6

  解析

• 4．将抛物线y=-（x+1）²向左平移1个单位后，得到的抛物线的顶点坐标是（　　）

  A．（-2，0）

  B．（0，0）

  C．（-1，-1）

  D．（-2，-1）
  组卷：133引用：4难度：0.9

  解析

• 5．已知二次函数

  y

  1

  =

  a

  x

  2

  +

  bx

  +

  c

  （

  a

  ≠

  0

  ）

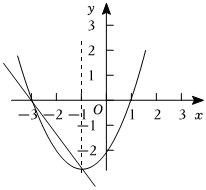  和一次函数y₂=kx+n（k≠0）的图象如图所示，下面有四个推断：
  ①二次函数y₁有最大值；
  ②当x＞-1时，二次函数y₁的图象y随x的增大而增大；
  ③当x=-2时，二次函数y₁的值大于0；
  ④过动点P（m,0）且垂直于x轴的直线与y₁，y₂的图象的交点分别为C，D，当点C位于点D上方时，m的取值范围是m＜-3或m＞-1．
  其中正确的是（　　）

  A．①③

  B．①④

  C．②④

  D．②③
  组卷：69引用：1难度：0.5

  解析

• 6．某型号的手机连续两次降价，每个售价由原来的1185元降到了580元，设平均每次降价的百分率为x,列出方程正确的是（　　）

  A．580（1+x）2=1185	B．1185（1+x）2=580
  C．580（1-x）2=1185	D．1185（1-x）2=580
  组卷：950引用：144难度：0.9

  解析

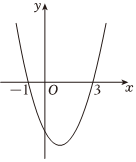• 7．二次函数y=ax²+bx+c的图象如图所示，下列说法正确的个数有（　　）
  ①a+b+c＞0；
  ②ab＞0；
  ③b+2a=0；
  ④方程ax²+bx+c=5有两个不相等的实数根．

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：31引用：1难度：0.5

  解析

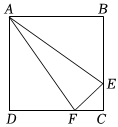• 8．如图，正方形ABCD中，AB=4cm,点E、F同时从C点出发，以1cm/s的速度分别沿CB-BA、CD-DA运动，到点A时停止运动．设运动时间为t（s），△AEF的面积为S（cm²），则S（cm²）与t（s）的函数关系可用图象表示为（　　）

  A．	B．
  C．	D．
  组卷：1496引用：15难度：0.7

  解析

二、填空题

• 9．在平面直角坐标系中点B的坐标为（3，1），点B关于原点的对称点的坐标为

  ．
  组卷：59引用：7难度：0.9

  解析

三、解答题

• 27．小明在学习时遇到这样一个问题：
  如果二次函数y=a₁x²+b₁x+c₁（a₁≠0，a₁，b₁，c₁是常数）与y=a₂x²+b₂x+c₂（a₂≠0，a₂，b₂，c₂是常数）满足a₁+a₂=0，b₁=b₂，c₁+c₂=0，则称这两个函数互为“旋转函数”．求y=-x²+3x-2函数的“旋转函数”．
  小明是这样思考的：由y=-x²+3x-2函数可知a₁=-1，b₁=3，c₁=-2，根据a₁+a₂=0，b₁=b₂，c₁+c₂=0，求出a₂，b₂，c₂，就能确定这个函数的“旋转函数”．
  请参考小明的方法解决下面的问题：
  （1）写出函数y=-x²+3x-2的“旋转函数”；
  （2）若函数y=-x²+

  4

  3

  mx-2与y=x²-2nx+n互为“旋转函数”，求（m+n）²⁰¹⁶的值；
  （3）已知函数y=-

  1

  2

  （x+1）（x-4）的图象与x轴交于A，B两点，与y轴交于点C，点A，B，C关于原点的对称点分别是A₁，B₁，C₁，试证明经过点A₁，B₁，C₁的二次函数与函数y=-

  1

  2

  （x+1）（x-4）互为“旋转函数”．
  组卷：105引用：2难度：0.3

  解析

• 28．正方形ABCD中，将边AB所在直线绕点A逆时针旋转一个角度α得到直线AM，过点C作CE⊥AM，垂足为E，连接BE．
  （1）当0°＜α＜45°时，设AM交BC于点F，
  ①如图1，若α=35°，则∠BCE=

  °；
  ②如图2，用等式表示线段AE，BE，CE之间的数量关系，并证明；
  （2）当45°＜α＜90°时（如图3），请直接用等式表示线段AE，BE，CE之间的数量关系．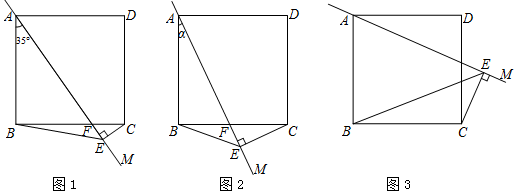
  
  组卷：872引用：7难度：0.4

  解析