2020-2021学年重庆市永川区萱花中学九年级（上）期中数学试卷
发布：2025/10/30 22:0:12
一、选择题（每小题4分，共48分）
-
1．证明命题“对于任意实数x,x2+5x+4的值总是正数”是假命题的反例可以是（ ）
组卷：131引用：2难度：0.6 -
2．二次函数y=ax2+b的图象如图所示，则一次函数y=ax+b的图象可能是（ ）组卷：1881引用：7难度：0.6 -
3．我们知道方程x2+2x-3=0的解是x1=1，x2=-3，现给出另一个方程（2x+3）2+2（2x+3）-3=0，它的解是（ ）
组卷：9346引用：70难度：0.7 -
4．将抛物线y=2x2向上平移5个单位长度，再向左平移2个单位长度，得到的抛物线关于x轴对称的函数表达式是（ ）
组卷：116引用：1难度：0.6 -
5．平面内有两点P，O，⊙O的半径为5，若PO=4，则点P与⊙O的位置关系是（ ）
组卷：1759引用：20难度：0.8 -
6．下列三个函数：①y=x+1；②
；③y=x2-x+1．其图象既是轴对称图形，又是中心对称图形的个数有（ ）y=1x组卷：631引用：60难度：0.7 -
7．已知点P的坐标为（x,y）且
，则点P关于原点的对称点P′的坐标是（ ）（x+1）2+2y+3=0组卷：110引用：2难度：0.9 -
8．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
组卷：14引用：1难度：0.8 -
9．方程x2+kx-1=0根的情况是（ ）
组卷：110引用：27难度：0.9 -
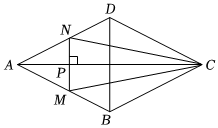10．如图，点P是菱形ABCD的对角线AC上的一个动点，过点P垂直于AC的直线交菱形ABCD的边于M、N两点．设AC=2，BD=1，AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是（ ）组卷：1857引用：15难度：0.7 -
11．天猫某店铺第2季度的总销售额为331万元，其中4月份的销售额是100万元，设5，6月份的平均月增长率为x,则可列方程为（ ）
组卷：855引用：4难度：0.9 -
12．程老师制作了如图1所示的学具，用来探究“边边角条件是否可确定三角形的形状”问题．操作学具时，点Q在轨道槽AM上运动，点P既能在以A为圆心、以8为半径的半圆轨道槽上运动，也能在轨道槽QN上运动．图2是操作学具时，所对应某个位置的图形的示意图．
有以下结论：
①当∠PAQ=30°，PQ=6时，可得到形状唯一确定的△PAQ；
②当∠PAQ=30°，PQ=9时，可得到形状唯一确定的△PAQ；
③当∠PAQ=90°，PQ=10时，可得到形状唯一确定的△PAQ；
④当∠PAQ=150°，PQ=12时，可得到形状唯一确定的△PAQ．
其中所有正确结论的序号是（ ）组卷：1382引用：14难度：0.7
二、填空题（每小题4分，共24分）
-
13．一元二次方程x2=x的解为．
组卷：1309引用：67难度：0.9 -
14．若点A（-1，m）和B（-2，n）在二次函数y=-x2+20图象上，则m n（填大小关系）．
组卷：178引用：2难度：0.5 -
15．抛物线y=ax2+bx+c（a,b,c为常数，且a≠0）经过点（-1，0）和（m,0），且1＜m＜2，当x＜-1时，y随着x的增大而减小．下列结论：①abc＞0；②a+b＞0；③若点A（-3，y1），点B（3，y2）都在抛物线上，则y1＜y2；④a（m-1）+b=0；⑤若c≤-1，则b2-4ac≤4a.其中结论错误的是．（只填写序号）
组卷：5567引用：61难度：0.7 -
16．如图，把一个直角三角形ACB绕着30°角的顶点B顺时针旋转，使点A与CB的延长线上的点E重合，这时旋转角的度数是 ．组卷：79引用：3难度：0.7 -
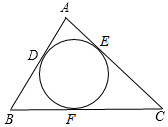17．如图，⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F，如果AB=4，AC=5，AD=1，那么BC的长为．组卷：2744引用：6难度：0.7 -
18．在平面直角坐标系中，已知A（-1，m）和B（5，m）是抛物线y=x2+bx+1上的两点，将抛物线y=x2+bx+1向上平移n（n是正整数）个单位，使平移后的图象与x轴没有交点，则n的最小值为 ．
组卷：2617引用：9难度：0.5
三、解答题（共78分）
-
19．如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均在格点上，点A的坐标为（2，3），点B的坐标为（3，0），点C的坐标为（0，2）．
（1）以点C为旋转中心，将△ABC旋转180°后得到△A1B1C1，请画出△A1B1C1；
（2）平移△ABC，使点A的对应点A2的坐标为（0，-1），请画出△A2B2C2．
（3）若将△A1B1C1绕点P旋转可得到△A2B2C2，则点P的坐标为 ．组卷：1883引用：18难度：0.7 -
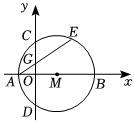20．如图，在平面直角坐标系xOy中，点M在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴于C、D两点，且C为弧AE的中点，AE交y轴于G点，若点A的坐标为（-2，0），AE=6．
（1）求证：CG=AG；
（2）求点C的坐标以及AC的长；
（3）连接MG、BC，求证：MG∥BC．组卷：50引用：2难度：0.5 -
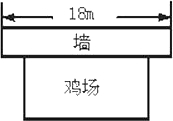21．如图，某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长18m），另三边用木栏围成，木栏长35m.
（1）鸡场的面积能达到150m2吗？
（2）鸡场的面积能达到180m2吗？
如果能，请你给出设计方案；如果不能，请说明理由．组卷：1049引用：16难度：0.1 -
22．已知关于x的一元二次方程x2-2x+m2-m=0有两个相等的实数根，求m的值．
组卷：196引用：3难度：0.5 -
23．用适当的方法解方程x2-5x+6=0．
组卷：494引用：22难度：0.3 -
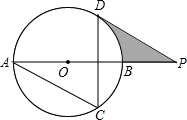24．如图，AB为⊙O的直径，AC、DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°．
（1）求证：DP是⊙O的切线；
（2）若⊙O的半径为3cm,求图中阴影部分的面积．组卷：1301引用：97难度：0.5 -
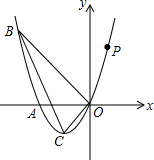25．如图，已知抛物线经过点A（-2，0），点B（-3，3）及原点O，顶点为C．
（1）求抛物线的解析式；
（2）在抛物线的BC段上，是否存在一点G，使得△GBC的面积最大？若存在，求出这个最大值及此时点G的坐标；若不存在，请说明理由；
（3）P是抛物线的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由；
（4）若点D在抛物线上，点E在抛物线的对称轴上，且以A、O、D、E为顶点的四边形是平行四边形，请直接写出点D的坐标．组卷：410引用：2难度：0.3 -
26．如图1，在平面直角坐标系，AB⊥x轴于点B，点A（a,b）满足
+（b-4）2=0．a-4
（1）点A坐标为；
（2）一个动点P从点B出发以每秒一个单位长度的速度沿射线BO一直向左运动，以BP为边长作正方形BPMQ，点M在射线BA上，设运动时间为t（t＞0），正方形BMQP与△AOB重叠面积为S，直接写出S关于t的解析式及t的取值范围；
（3）如图2，AB垂直x轴于点B，点A的坐标变为了（2，4），平移线段AB使点A与原点重合，点B的对应点为点C．E是线段OB上一动点，以OB为边作∠BOG=∠AOB，交BC于点G，连CE交OG于点F，当点E在线段OB上运动过程中，的值是否会发生变化？若变化请说明理由，若不变，请求出其值．∠OFC+∠FCG∠OEC
组卷：216引用：2难度：0.4
