当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省鞍山市岫岩县九年级（下）月考数学试卷（3月份）

发布：2024/7/5 8:0:9

一、选择题（每小题3分，共24分）

1．一元二次方程x²-2x-3=0的二次项系数、一次项系数、常数项分别是（　　）
A．1，-2，-3 B．1，-2，3 C．1，2，3 D．1，2，-3
组卷：429引用：23难度：0.9
解析
2．下列图形中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：3引用：1难度：0.9
解析
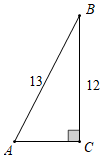3．如图，在Rt△ABC中，∠C=90°，AB=13，BC=12，下列三角函数正确的是（　　）
A．sinB=
12
13
B．cosA=
12
13
C．tanB=
5
12
D．cosB=
12
5
组卷：1812引用：9难度：0.5
解析
4．若反比例函数y=
k
x
（k≠0）的图象经过点（2，-3），则它的图象也一定经过的点是（　　）
A．（-2，-3） B．（-3，-2） C．（1，-6） D．（6，1）
组卷：1569引用：20难度：0.5
解析
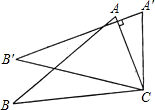5．如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在B′位置，A点落在A′位置，若AC⊥A′B′，则∠BAC的度数是（　　）
A．50° B．60° C．70° D．80°
组卷：1063引用：115难度：0.9
解析
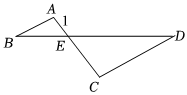6．如图，AB∥CD，AC、BD相交于点E．AE=1，EC=2，DE=3，则BD的长为（　　）
A．
3
2
B．4 C．
9
2
D．6
组卷：371引用：8难度：0.6
解析
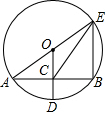7．如图，⊙O的半径OD垂直于弦AB，垂足为点C，连接AO并延长交⊙O于点E，连接BE，CE．若AB=8，CD=2，则△BCE的面积为（　　）
A．12 B．15 C．16 D．18
组卷：3314引用：19难度：0.7
解析
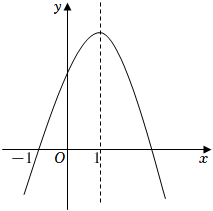8．如图，已知开口向下的抛物线y=ax²+bx+c与x轴交于点（-1，0），对称轴为直线x=1．则下列结论正确的有（　　）
①abc＞0；
②2a+b=0；
③函数y=ax²+bx+c的最大值为-4a；
④若关于x的方程ax²+bx+c=a+1无实数根，则-
1
5
＜a＜0．
A．1个 B．2个 C．3个 D．4个
组卷：1849引用：20难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

七、解答题（共12分）

25．问题背景：
一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知AD是△ABC的角平分线，可证
AB
AC
=
BD
CD
．小慧的证明思路是：如图2，过点C作CE∥AB，交AD的延长线于点E，构造相似三角形来证明
AB
AC
=
BD
CD
．
尝试证明：
（1）请参照小慧提供的思路，利用图2证明：
AB
AC
=
BD
CD
；
应用拓展：
（2）如图3，在Rt△ABC中，∠BAC=90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，点C恰好落在边AB上的E点处．
①若AC=1，AB=2，求DE的长；
②若BC=m,∠AED=α，求DE的长（用含m,α的式子表示）．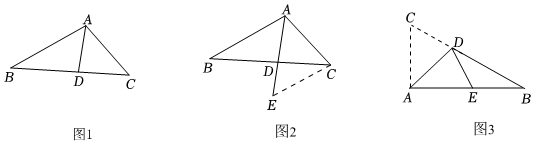
组卷：2561引用：18难度：0.4
解析

八、解答题（共14分）

26．如图，已知抛物线：y=-2x²+bx+c与x轴交于点A，B（2，0）（A在B的左侧），与y轴交于点C，对称轴是直线x=
1
2
，P是第一象限内抛物线上的任一点．
（1）求抛物线的解析式；
（2）若点D为线段OC的中点，则△POD能否是等边三角形？请说明理由；
（3）过点P作x轴的垂线与线段BC交于点M，垂足为点H，若以P，M，C为顶点的三角形与△BMH相似，求点P的坐标．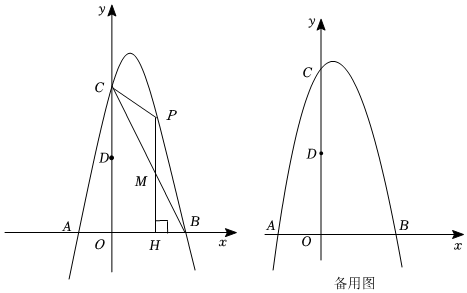
组卷：2724引用：8难度：0.3
解析