2022-2023学年重庆八中九年级（上）期中数学试卷

一、选择题：在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

• 1．-6的相反数是（　　）

  A．-6

  B． - 1 6

  C．6

  D． 1 6
  组卷：2397引用：87难度：0.8

  解析

• 2．下列图形中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：13引用：2难度：0.9

  解析

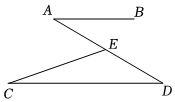• 3．如图所示，已知AB∥CD，点E在线段AD上（不与点A、点D重合），连接CE．若∠C=15°，∠AEC=60°．则∠A的值为（　　）

  A．45°

  B．75°

  C．46°

  D．76°
  组卷：199引用：6难度：0.7

  解析

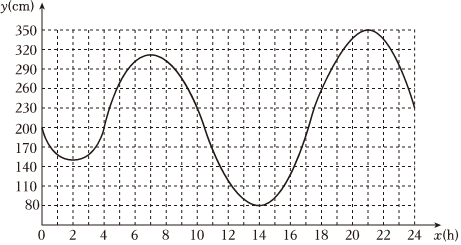• 4．如图，曲线表示某港口的湖水高度y（cm）随时间x（h）的变化情况，则这个港口水位最低的时刻约为（　　）

  A．2时

  B．7时

  C．14时

  D．21时
  组卷：10引用：1难度：0.8

  解析

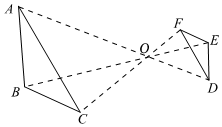• 5．如图，△ABC与△DEF是位似图形，点O为位似中心，已知BO：OE=2：1，则△ABC与△DEF的面积比是（　　）

  A．2：1

  B．3：1

  C．4：1

  D．5：1
  组卷：571引用：9难度：0.4

  解析

• 6．用火柴棒按下面的方式搭图形，按照这样的规律搭下去，第⑦个图形需要的火柴棒的根数是（　　）
  

  A．32

  B．37

  C．42

  D．47
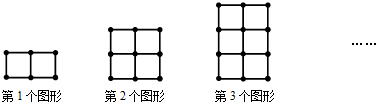  组卷：242引用：5难度：0.5

  解析

• 7．估计

  2

  ×

  3

  -

  24

  的值应在（　　）

  A．2和3之间

  B．3和4之间

  C．-3和-4之间

  D．-3和-2之间
  组卷：17引用：2难度：0.8

  解析

• 8．某市2019年年底自然保护区覆盖率（即自然保护区面积占全市国土面积的百分比）仅为12%，经过两年努力，该市2021年年底自然保护区覆盖率达到17.28%，设年均增长率为x.则根据题意，下面所列方程正确的是（　　）

  A．12%（1+x）=17.28%	B．12%（1+x）2=17.28%
  C．12%（1-x）=17.28%	D．12%（1-x）2=17.28%
  组卷：34引用：1难度：0.5

  解析

三、解答题：解答时每小题必须给出必要的演算过程或推理步骤，面出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

• 24．如图，在平面直角坐标系中，抛物线y=x²+bx+c与x轴交于点A、C，与y轴交于点B，已知A（-1，0），B（0，-2），连接AB．
  
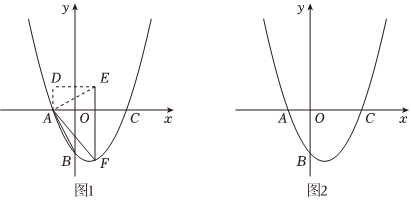
  （1）求该抛物线的解析式；
  （2）如图1，将△AOB绕点A逆时针旋转90得到△ADE，在该抛物线上有一点F，F在第四象限，求四边形AFED面积的最大值及此时F的坐标；
  （3）如图2，若将原抛物线y=x²+bx+c向左平移2个单位，向上平移3个单位得到新的抛物线y′，新的抛物线y′与y轴交于点G．点H为原抛物线上的一点，且横坐标为1，点M为新抛物线y′对称轴上的一点，在新抛物线y′上确定一点N，使得以点G、H、M、N为顶点的四边形是平行四边形，请直接写出新抛物线y′的解析式和所有满足条件的N的坐标．
  组卷：69引用：1难度：0.1

  解析

• 25．在△ABC中，已知AB=AC，作AM⊥BC，D是AM上一点，∠DBC=30°，连接BD、CD，在BD上截取DE=AD，连接AE．
  
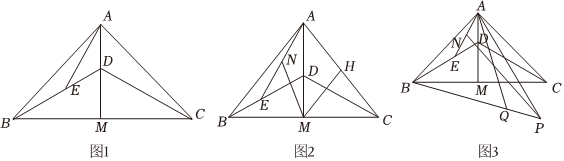
  （1）如图1所示，若∠BAC=90°，AD=

  3

  ，求△ABE的周长；
  （2）如图2所示，若分别取AE、AC的中点N、H，连接MN、MH，求证：MN=MH；
  （3）如图3所示，∠BAC=90°，BC=2，将AC沿着直线AP翻折得到AQ，连接BQ，直线BQ交AP于点P，N为AE中点，当PN取得最小值时，请直接写出△APN的面积．
  组卷：198引用：1难度：0.1

  解析