2022-2023学年湖南省岳阳市华容县八年级(下)期末数学试卷
发布:2024/7/17 8:0:9
一、选择题(每小题3分,共24分)
-
1.在平面直角坐标系中,点(5,-3)关于x轴对称的点的坐标是( )
组卷:86引用:4难度:0.8 -
 2.如图,在△ABC中,BC=4,点D,E分别为AB,AC的中点,则DE=( )组卷:1463引用:13难度:0.8
2.如图,在△ABC中,BC=4,点D,E分别为AB,AC的中点,则DE=( )组卷:1463引用:13难度:0.8 -
3.将函数y=2x的图象向上平移3个单位,则平移后的函数解析式是( )
组卷:1184引用:13难度:0.9 -
4.下列关于数字变换的图案中,既是轴对称图形又是中心对称图形的是( )
组卷:45引用:5难度:0.8 -
5.一次函数y=kx+b的图象经过第一、三、四象限,则( )
组卷:504引用:67难度:0.9 -
6.下列说法错误的是( )
组卷:329引用:3难度:0.5 -
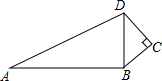 7.如图,已知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )组卷:1531引用:5难度:0.9
7.如图,已知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )组卷:1531引用:5难度:0.9 -
8.定义:对于给定的一次函数y=ax+b(a、b为常数,且a≠0),把形如
的函数称为一次函数y=ax+b的“衍生函数”,已知一次函数y=2x-1,若点P(-2,m)在这个一次函数的“衍生函数”图象上,则m的值是( )y=ax+b(x≥0)-ax+b(x<0)组卷:127引用:3难度:0.7
三、解答题(本大题8道小题满分64分,解答应写出文字说明、证明过程或演算步骤)
-
23.在正方形ABCD中,线段EF交对角线AC于点G.
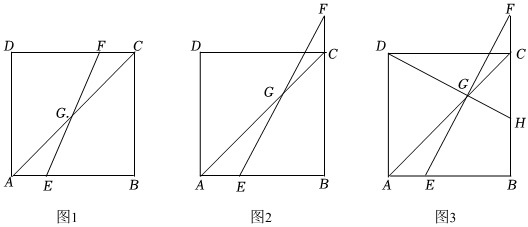
(1)如图1,若点E、F分别在AB、CD边上,且AE=CF,求证:FG=EG;
(2)如图2,若点E在AB边上,点F在BC边的延长线上,且AE=CF.(1)中结论是否依然成立?请说明理由;
(3)在(2)的条件下,连接DG并延长交BC于点H,若BH=3,BE=4.求正方形ABCD的面积.组卷:97引用:2难度:0.5 -
24.建立模型:
如图1,等腰Rt△ABC中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.
模型应用:
(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.
①若∠ABC=90°,且点C在第一象限,求点C的坐标;
②若AB为直角边,求点C的坐标;
(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.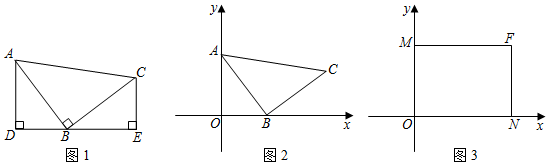 组卷:1792引用:4难度:0.2
组卷:1792引用:4难度:0.2


