当前位置：试卷中心 > 试卷详情

2022-2023学年甘肃省天水市秦安五中、兴国中学等三校八年级（下）期末数学试卷

发布：2024/7/7 8:0:9

一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项.

1．下列各式-x,
2
π
，-
3
x
-
2
，
x
x
2
-
1
中，分式有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：231引用：2难度：0.5
解析
2．0.0000205用科学记数法表示为（　　）
A．2.05×10^-7 B．2.05×10^-6 C．2.05×10^-5 D．2.05×10^-4
组卷：38引用：4难度：0.9
解析
3．点P（3，-4）关于y轴的对称点P′的坐标是（　　）
A．（-3，-4） B．（3，4） C．（-3，4） D．（-4，3）
组卷：1663引用：28难度：0.9
解析
4．菱形具有而矩形不一定具有的性质是（　　）
A．对边平行 B．对角线互相平分
C．对角线互相垂直 D．对角互补
组卷：884引用：8难度：0.7
解析
5．若关于x的分式方程
3
-
x
x
-
5
-
m
5
-
x
=0有增根，则m的值为（　　）
A．2 B．3 C．5 D．-2
组卷：614引用：3难度：0.4
解析
6．已知A（1，y₁），B（2，y₂）两点在双曲线y=
3
+
2
m
x
上，且y₁＞y₂，则m的取值范围是（　　）
A．m＜0 B．m＞0 C．m＞-
3
2
D．m＜-
3
2
组卷：429引用：7难度：0.9
解析
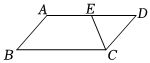7．如图，在平行四边形ABCD中，AD=7，CE平分∠BCD交AD边于点E，且AE=4，则AB的长为（　　）
A．4 B．3 C．
5
2
D．2
组卷：2645引用：7难度：0.9
解析
8．在同一坐标系中，函数
y
=
k
x
和y=kx-2的图象大致是（　　）
A． B．
C． D．
组卷：1011引用：5难度：0.6
解析
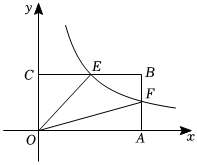9．如图，已知双曲线
y
=
k
x
（
x
＞
0
）
经过矩形OABC边AB的中点F且交BC于E，四边形OEBF的面积为2，则k=（　　）
A．1 B．2 C．4 D．8
组卷：191引用：1难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共5小题，共50分，解答时，应写出必要的文字说明、证明过程或者演算步骤.

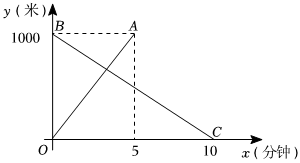26．一条笔直的路上依次有M，P，N三地，其中M，N两地相距1000米．甲、乙两机器人分别从M，N两地同时出发，去目的地N，M，匀速而行．图中OA，BC分别表示甲、乙机器人离M地的距离y（米）与行走时间x（分钟）的函数关系图象．
（1）求OA所在直线的表达式；
（2）出发后甲机器人行走多少时间，与乙机器人相遇？
（3）甲机器人到P地后，再经过1分钟乙机器人也到P地，求P，M两地间的距离．
组卷：3270引用：10难度：0.5
解析
27．【阅读材料】如图①，在边长为4的正方形ABCD中，点E、F分别在边BC、CD上且∠EAF=45°，连结EF，求△CEF的周长．

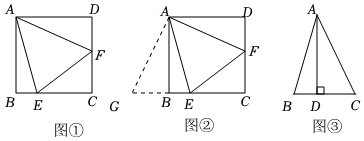
小明想到解决问题的方法如下：
如图②，延长CB至点G，使BG=DF，通过证明△AGE≌△AFE，得到BE、DF、EF之间的关系，进而求出△CEF的周长．
请按照小明的思路，帮助小明写出完整的求解过程．
【方法应用】如图②，若BE=1，求DF的长．
【能力提升】如图③，在锐角△ABC中，∠BAC=45°，AD⊥BC于点D．若BD=1，AD=4，则CD的长为
．
组卷：317引用：5难度：0.3
解析