2022-2023学年广东省惠州市惠城区小金茂峰学校九年级（上）期中数学试卷

一．选择题（共10小题，30分）

• 1．在平面直角坐标系中，点（2，-3）关于原点的对称点的坐标是（　　）

  A．（-2，3）

  B．（-2，-3）

  C．（2，3）

  D．（-3，2）
  组卷：486引用：11难度：0.8

  解析

• 2．取5张扑克牌，其中1张“黑桃”，2张“梅花”和2张“红桃”，将这些扑克牌背面朝上从中任抽一张，恰好是“梅花”的概率是（　　）

  A． 1 5

  B． 1 3

  C． 2 5

  D． 3 5
  组卷：105引用：3难度：0.7

  解析

• 3．用配方法解方程x²+2x=3时，配方后正确的是（　　）

  A．（x+2）2=7

  B．（x+2）2=5

  C．（x+1）2=4

  D．（x+1）2=2
  组卷：733引用：6难度：0.6

  解析

• 4．将二次函数y=（x-1）²+2的图象向上平移3个单位，得到的图象对应的函数表达式是（　　）

  A．y=（x+2）2+2

  B．y=（x-1）2+5

  C．y=（x-4）2+2

  D．y=（x-1）2-1
  组卷：205引用：4难度：0.8

  解析

• 5．已知关于x的一元二次方程（k-1）x²-2x+1=0有两个不相等的实数根，则k的取值范围是（　　）

  A．k＞2

  B．k＞2且k≠1

  C．k＜2

  D．k＜2且k≠1
  组卷：987引用：9难度：0.7

  解析

• 6．对于二次函数y=-4（x+6）²-5的图象，下列说法正确的是（　　）

  A．图象与y轴交点的坐标是（0，5）

  B．对称轴是直线x=6

  C．顶点坐标为（-6，5）

  D．当x＜-6时，y随x的增大而增大
  组卷：1644引用：14难度：0.7

  解析

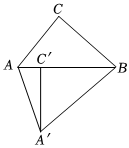• 7．如图，△ABC中，∠ACB=90°，∠ABC=40°．将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠AA′C′的度数是（　　）

  A．15°

  B．20°

  C．25°

  D．30°
  组卷：677引用：7难度：0.4

  解析

三．解答题（共8小题，75分）

• 22．在△ABC中，AC=BC=2，∠C=90°．将一块三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交边AC、CB于点D、E．
  （1）如图①，当PD⊥AC时，则DC+CE的值是

  ．
  （2）如图②，当PD与AC不垂直时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；
  （3）如图③，在∠DPE内作∠MPN=45°，使得PM、PN分别交DC、CE于点M、N，连接MN．那么△CMN的周长是否为定值？若是，求出定值；若不是，请说明理由．
  
  组卷：394引用：2难度：0.5

  解析

• 23．如图，已知抛物线y=ax²+bx+c（a≠0）与x轴交于点A（1，0）和点B（-3，0），与y轴交于点C，且OC=OB．
  （1）求点C的坐标和此抛物线的解析式；
  （2）若点E为第二象限抛物线上一动点，连接BE，CE，BC，求△BCE面积的最大值；
  （3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．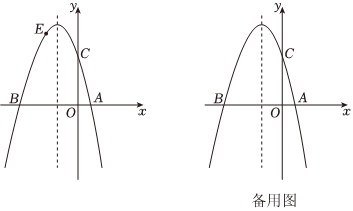
  
  组卷：3663引用：14难度：0.1

  解析